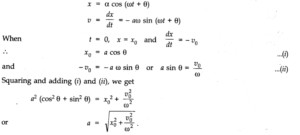Question 14. 1. Which of the following examples represent periodic motion?
(a) A swimmer completing one (return) trip from one bank of a river to the other and back.
(b) A freely suspended bar magnet displaced from its N-S direction and released.
(c) A hydrogen molecule rotating about its centre of mass.
(d) An arrow released from a bow.
Answer:(a) It is not a periodic motion. Though the motion of a swimmer is to and fro but will not have a definite period.
(b) Since a freely suspended magnet if once displaced from N-S direction and released, it oscillates about this position, it is a periodic motion.
(c) The rotating motion of a hydrogen molecule about its centre of mass is periodic.
(d) Motion of an arrow released from a bow is non-periodic.
Question 14. 2. Which of the following examples represent (nearly) simple harmonic motion and which represent
periodic but not simple harmonic motion?
(a) the rotations of earth about its axis.
(b) motion of an oscillating mercury column in a U-tube.
(c) motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lowermost point.
(d) general vibrations of a polyatomic molecule about its equilibrium position.
Answer:(a) Since the rotation of earth is not to and fro motion about a fixed point, thus it is periodic but not S.H.M.
(b) It is S.H.M.
(c) It is S.H.M.
(d) General vibrations of a polyatomic molecule about its equilibrium position is periodic but non SHM. In fact, it is a result of superposition of SHMs executed by individual vibrations of atoms of the molecule.
Question 14. 3. Fig. depicts four x-t plots for linear motion of a particle. Which of ike plots represent periodic motion? What is the period of motion (in case of periodic motion)?

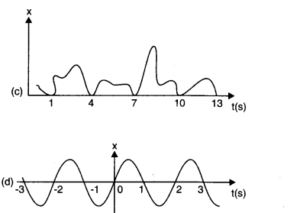
Answer:Figure (b) and (d) represent periodic motions and the time period of each of these is 2 seconds, (a) and (c) are non-periodic motions.
Question 14. 4. Which of the following function of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (to is any positive constant).
(a) sin wt – cos wt (b) sin2wt (c) 3 cos -2 cos (π/4-2 wt) (d) cos wt + cos 3 wt + cos 5 wt
(e) exp (- w2t2) (f) 1 + wt + w2t2.
Answer:The function will represent a periodic motion, if it is identically repeated after a fixed interval of time and will represent S.H.M if it can be written uniquely in the form of a cos

(e) e-w2t2. It is an exponential function which never repeats itself. Therefore it represents non-periodic motion.
(f) 1 + wt + w2t2also represents non periodic motion.
Question 14. 5. A particle is in linear simple harmonic motion between two points, A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is
(a) at the end A,
(b) at the end B,
(c) at the mid-point of AB going towards A,
(d) at 2 cm away from B going towards A,
(e) at 3 cm away from A going towards B, and (f) at 4 cm away from B going towards A.
Answer:In the fig. (given below), the points A and B, 10 cm apart, are the extreme positions of the particle in SHM, and the point O is the mean position. The direction from A to B is positive, as indicated.
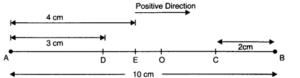
(a) At the end A, i.e., extreme position, velocity is zero, acceleration and force are directed towards O and are positive.
(b) At the end B, i.e., second extreme position, velocity is zero whereas the acceleration and force are directed towards the point O and are negative.
(c) At the mid point O, while going towards A, velocity is negative and maximum. The acceleration and force both are zero.
(d) At 2 cm away from B, that is, at C and going towards A: v is negative; acceleration and F, being directed towards O, are also negative.
(e) At 3 cm away from A, that is, at D and going towards B: v is positive; acceleration and F, being directed towards O, are also positive.
(f) At a distance of 4 cm away from A and going towards A, velocity is directed along BA, therefore, it is positive. Since acceleration and force are directed towards OB, both of them are positive.
Question 14. 6. Which of the following relationships between the acceleration a and the displacement x of a particle involve simple harmonic motion?
(a) a = 0.7x (b) a = – 200 x2
(c) a = – 10x (d) a = 100 x3
Answer:Only (c) i.e., a = – 10x represents SHM. This is because acceleration is proportional and opposite to displacement (x).
Question 14. 7. The motion of a particle executing simple harmonic motion is described by the displacement function.x(t) = A cos (wt +Ф ).If the initial (t = 0) position of the particle is 1 cm and its initial velocity is w cm/s, what are its amplitude and initial phase angle? The angular frequency of the particle is π s-1. If instead of the cosine function, we choose the sine function to describe the SHM: x = B sin (wt + α), what are the amplitude and initial phase of the particle with the above initial conditions?
Answer:

Question 14. 8. A spring balance has a scale that reads from 0 to 50 kg. The length of the scale is 20 cm. A body suspended from this balance, when displaced and released, oscillates with a period of 0.6 s. What is the weight of the body?
Answer:
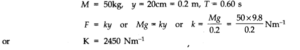
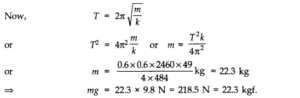
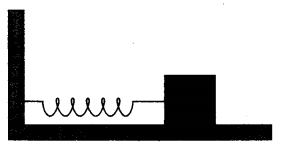
Question 14. 9. A spring having with a spring constant 1200 Nm-1is mounted on a horizontal table as shown in Fig. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released. Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
Answer:

Question 14. 10. In Exercise 9, let us take the position of mass when the spring is unstreched as x = 0, and the direction from left to right as the positive direction of x – axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch (t = 0), the mass is(a)at the mean position,(b)at the maximum stretched position, and(c)at the maximum compressed position.In what way do these functions for SHM differ from each other, in frequency, in amplitude or the initial phase?
Answer:

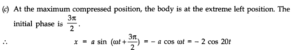
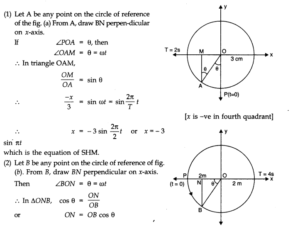
Question 14. 11. The following figures correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e., clockwise or anticlockwise) are indicated on each figure.

Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P in each case.
Answer:
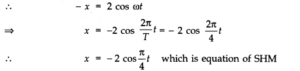
Question 14. 12. Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t = 0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anti-clockwise in every case:
(x is in cm and t is in s)
(a) x = – 2 sin (3t + π /3)
(b) x = cos (π /6 – t)
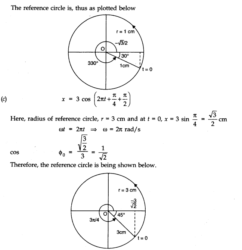
(c) x = 3 sin (2πt + π /4)
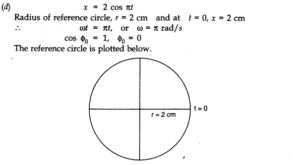
(d) x = 2 cos π t.
Answer:

Question 14. 13. Figure (a) shows a spring of force constant k clamped rigidly at one end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure (b) shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in Figure – (b) is stretched by the same force F.
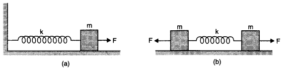
(a) What is the maximum extension of the spring in the two cases?
(b) If the mass in Fig. (a) and the two masses in Fig. (b) are released free, what is the period of oscillation in each case?
Answer:

Question 14. 14. The piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of 1.0 m. If the piston moves with simple harmonic motion with an angular frequency of 200 rev/min, what its maximum speed?
Answer:
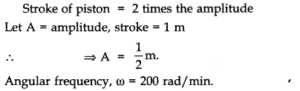
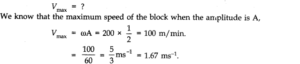
Question 14. 15. The acceleration due to gravity on the surface of moon is 1.7 ms-2. What is the time period of a simple pendulum on the surface of moon if its time-period on the surface of Earth is 3.5 s? (g on the surface of Earth is 9.8 ms-2.)
Answer:

Question 14. 16.

Answer:

(c) The wristwatch uses an electronic system or spring system to give the time, which does not change with acceleration due to gravity. Therefore, watch gives the correct time.
(d) During free fall of the cabin, the acceleration due to gravity is zero. Therefore, the frequency of oscillations is also zero i.e., the pendulum will not vibrate at all.
Question 14. 17. A simple pendulum of length l and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period?
Answer:In this case, the bob of the pendulum is under the action of two accelerations.

Question 14. 18. A cylindrical piece of cork of density of base area A and height h floats in a liquid of density ρ1. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
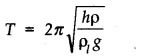
where ρ is the density of cork. (Ignore damping due to viscosity of the liquid).
Answer:
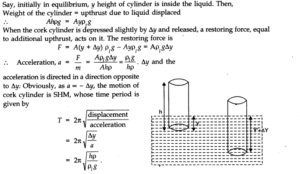
Question 14. 19. One end of a U-tube containing mercury is connected to a suction pump and the other end to the atmosphere.
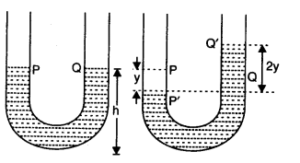
A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.
Answer:The suction pump creates the pressure difference, thus mercury rises in one limb of the U-tube. When it is removed, a net force acts on the liquid column due to the difference in levels of mercury in the two limbs and hence the liquid column executes S.H.M. which can be expressed as:
Consider the mercury contained in a vertical U-tube upto the level P and Q in its two limbs.
Let P = density of the mercury.
L = Total length of the mercury column in both the limbs.
A = internal cross-sectional area of U-tube. m = mass of mercury in U-tube = LAP.
Assume, the mercury be depressed in left limb to F by a small distance y, then it rises by the same amount in the right limb to position Q’.
.’. Difference in levels in the two limbs = P’ Q’ = 2y.
:. Volume of mercury contained in the column of length 2y = A X 2y
.•. m – A x 2y x ρ.
If W = weight of liquid contained in the column of length 2y.
Then W = mg = A x 2y x ρ x g
This weight produces the restoring force (F) which tends to bring back the mercury to its equilibrium position.

Question 14. 20. An air chamber of volume V has a neck area of cross-section into which a ball of mass m just fits and can move up and down without any friction (Fig.). Shaw that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal.
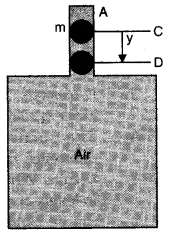
Answer:Consider an air chamber of volume V with a long neck of uniform area of cross-section A, and a frictionless ball of mass m fitted smoothly in the neck at position C, Fig. The pressure of air below the ball inside the chamber is equal to the atmospheric pressure.
Increase the pressure on the ball by a little amount p, so that the ball is depressed to position D, where CD = y.
There will be decrease in volume and hence increase in pressure of air inside the chamber. The decrease in volume of the air inside the chamber, ΔV = Ay

![]()
Note.If the ball oscillates in the neck of chamber under isothermal conditions, thru E = P = picture of air inside the chamber, when ball is at equilibrium position. If the ball oscillate in the neck of chamber under adiabatic conditions, then E = gP. where g = Cp/Cv.
Question 14. 21. You are riding an automobile of mass 3000 kg. Assuming that you are examining the oscillation characteristics of its suspension system. The suspension sags 15 cm when the entire automobile is placed on it. Also, the amplitude of oscillation decreases by 50% during one complete oscillation. Estimate the values of (a) the spring constant k and (b) the damping constant b for the spring and shock absorber system of one wheel, assuming that each wheel supports 750 kg. g = 10 m/s2.
Answer:

Question 14. 22. Show that for a particle in linear SHM the average kinetic energy over a period of oscillation equals the average potential energy over the same period.
Answer:Let the particle executing SHM starts oscillating from its mean position. Then displacement equation is
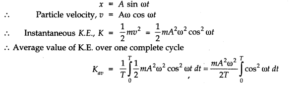

Question 14. 23. A circular disc, of mass 10 kg, is suspended by a wire attached to its centre. The wire is twisted by rotating the disc and released. The period of torsional oscillations of found to be 1.5 s. The radius of the disc is 15 cm. Determine the torsional spring constant of the wire. (Torsional spring constant) a is defined by the relation J = – αθ, where J is the restoring couple and θ the angle of twist).
Answer:
Question 14. 24. A body describes simple harmonic motion with an amplitude of 5 cm and a period of 0.2 s. Find the acceleration and velocity of the body when the displacement is (a) 5 cm (b) 3 cm (c) 0 cm
Answer:

Question 14. 25. A mass attached to a spring is free to oscillate, with angular velocity w, in a horizontal plane without friction or damping. It is pulled to a distance x0and pushed towards the centre with a velocity v0at time t = 0. Determine the amplitude of the resulting oscillations in terms of the parameters w, x0and v0.
Answer: