Chapter 15 – Plant Growth and Development Questions and Answers: NCERT Solutions for Class 11 Biology

1. Define growth, differentiation, development, dedifferentiation, development, redifferentiation, determinate growth, meristem and growth rate.

Solution:
Growth – it is an irreversible, permanent increase in the size of an organ or its parts or even of an individual cell. Growth is supplemented by metabolic activities taking place due to the energy.
Differentiation – The cells derived from root apical and shoot-apical meristems and cambium differentiate and mature to perform specific functions. This act leading to maturation is termed as differentiation.
Development – All the changes that an organisms goes through in its lifetime are called as development.
Dedifferentiation – Plants which has lost the capacity to divide can regain the capacity under certain conditions. This phenomenon is called as dedifferentiation. Example – meristem formation
Redifferentiation – Dedifferentiation produces cells that once again lose the capacity to divide but mature to perform specific functions are said to be redifferentiated.
Determinate growth – Ability of a cell, tissue or organism to grow for a certain period is called determinate growth. In most of the plants growth is indefinite, where some plants grow to a certain level and then stop growing.
Meristem – Plant tissue containing undifferentiated cells (meristematic cells) are called meristem.
Growth rate – Increase growth per unit time is called a growth rate.

2. Why is not anyone parameter good enough to demonstrate growth throughout the life of a flowering plant?

Solution:
Growth is a consequence of increase in the quantity of protoplasm. Measuring the protoplasmic growth includes several parameter, to name a few – increase in height, weight, number of cells, fresh tissue sample, length, area, volume etc. Hence it is difficult to demonstrate any one parameter of growth throughout the life of a flowering plant.

3. Describe briefly:
(a) Arithmetic growth
(b) Geometric growth
(c) Sigmoid growth curve
(d) Absolute and relative growth rates

Solution:
(a)In arithmetic growth, only one daughter cell continues to divide while the other differentiates and matures. The simplest expression of arithmetic growth is exemplified by a root elongating at a constant rate.

It can be mathematically expressed as follows:
Lt= LO+ rt
Lt= length of time ‘t’
LO= length at time ‘zero’
r= growth rate/elongation per unit time
(b)In geometric growth, the initial growth is slow (lag phase), and it increases rapidly after that – at an exponential rate (log or exponential phase). Here, both the progeny cells following mitotic cell division retain the ability to divide and continue to do so. The growth slows down due to limited nutrient supply leading to stationary phase. The number increases in a multiplicative pattern in geometric growth.

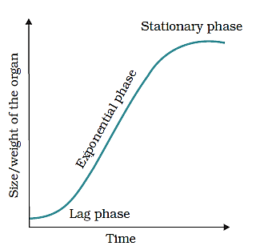
In geometric growth if we plot the parameter of growth against time, we get a typical sigmoid or S-curve.
Exponential growth can be expressed as:
W1= W0ert
W1= final size
W0= initial size of the period
r=growth rate
t=time growth
e=base of natural logarithms
‘r’ is the relative growth as well as the measure of the ability of plants to generate new plant substances which is termed as efficiency index. Thus, the final size of W1is dependant on the initial size W0
(c) Sigmoid growth curve
It is an S – shaped graph that is generated by plotting growth against time and has four main components – a slow lag phase, exponential phase or rapid phase, stage of diminishing growth and stationary phase.

(d) Absolute and relative growth rates – absolute growth rate is the net growth per unit time. Relative growth rate is the growth rate per unit time per unit initial growth.

4. List five main groups of natural plant growth regulators. Write a note on discovery, physiological functions and agricultural/horticultural applications of any one of them.

Solution:
Plant growth regulators are the intercellular intrinsic factors (chemical substances) that are responsible for the growth and development of plants. The five main groups of natural plant growth regulators (PGR) are as follows:
Auxins
Gibberellins
Cytokinins
Abscisic acid
Ethylene
These PGRs are synthesized in different plant parts, governing various differentiation and developmental events that take place in the life cycle of a plant.
Gibberellins
Discovery:
Denoted as GA1, GA2, GA3, gibberellic acid or GA3was one of the first gibberellins to be discovered, they are all acidic
There are more than 100 gibberellins reported from widely different entities such as fungi and other higher plants
Physiological functions
Gibberellins produce a wide range of physiological responses in plants
They can cause an increase in the length of grapes stalks as they are capable to bring about an increase in the length of axis
They cause fruits such as apples to elongate and improve its shape
They are responsible in delaying the process of senescence.
Agricultural/horticultural applications
As the senescence process is delayed, the fruits can be left on the tree for longer in order to extend the market period.
In brewing industry, gibberellic acid or GA3is used to speed up the malting process
As sugarcane stores carbohydrate as sugar in their stems, spraying the sugarcane crop with gibberellins causes the length of the stem to increase hence causing an increase in the yield by as much as 20 tonnes per acre
The maturity period of juvenile conifers can be hastened by spraying with GAs resulting in early seed production
It also promotes the process of bolting in beetroots, cabbages etc. Bolting is the internode elongation observed just before the flowering process.

5. What do you understand by photoperiodism and vernalisation? Describe their significance.

Solution:
Photoperiodism can be termed as the response of plants to periods of day/night. It is theorized that the hormonal substance that is responsible for flowering, is formed in the leaves which subsequently migrates to the shoot apices and alters them into flowering apices. This process of photoperiodism helps in studying the response of flowering in different crop plants when the duration of exposure of light is considered.
Vernalisation is the phenomena where the process of flowering in some plants is either quantitatively or qualitatively dependent on the exposure to lower temperatures. In particular, it refers to promoting the flowering process by a period of lower temperatures. The process prevents precocious reproductive development late in the growing season which thereby enables the plant to have sufficient time to attain maturity.

6. Why is abscisic acid also known as stress hormone?

Solution:
Abscisic acid is responsible to stimulate the closure of stomata in the epidermis and raises the tolerance of plants to different types of stresses, hence it is also called as stress hormone. Abscisic acid is responsible to promote seed dormancy thereby ensuring the germination of seeds during favorable conditions. This helps the seeds to withstand desiccation and to induce dormancy towards the end of the growing season in plants thereby promoting abscission of the fruits, leaves and flowers.

7. ‘Both growth and differentiation in higher plants are open’. Comment.

Solution:
The ability of higher plants to retain the capacity to have an indefinite growth through their life span is because of the presence of meristems at specific locations of their body. The cells as a result of these meristems have the capacity to divide and perpetuate on their own. This is why the growth in higher plants is open. Few of these cells undergo differentiation always subsequent to a few rounds of cell division. Thus, differentiation is open too.

8. ‘Both a short day plant and a long day plant can produce flower simultaneously in a given place’. Explain.

Solution:
In a few plants, flowering depends on relative durations of dark and light periods. Both the long-day plants and the short-day plants can flower at the same place with the condition being that they are supplied with sufficient photoperiod.

9. Which one of the plant growth regulators would you use if you are asked to:
(a) induce rooting in a twig
(b) quickly ripen a fruit
(c) delay leaf senescence
(d) induce growth in axillary buds
(e) ‘bolt’ a rosette plant
(f) induce immediate stomatal closure in leaves

Solution:
Listed below are the plant growth regulators for the corresponding events:
(a) induce rooting in a twig – Auxins
(b) quickly ripen a fruit – Ethylene
(c) delay leaf senescence – Cytokinins
(d) induce growth in axillary buds – Cytokinins
(e) ‘bolt’ a rosette plant – Gibberellins
(f) induce immediate stomatal closure in leaves – Abscisic acid

10. Would a defoliated plant respond to photoperiodic cycle? Why?

Solution:
No, a defoliated plant will not respond to photoperiodic cycle. This is because the leaves are the sites of perception of dark or light duration. Hence, if leaves were not present, plants would not respond to light.

11. What would be expected to happen if:
(a) GA3is applied to rice seedlings
(b) dividing cells stop differentiating
(c) a rotten fruit gets mixed with unripe fruits
(d) you forget to add cytokinin to the culture medium

Solution:
1. The rice seedlings will show internode-elongation and hence an increase in the height will be observed if GA3is applied to rice seedlings
2. If the dividing cells stop differentiating, the different plant parts such as the stem and leaves will not form.
3. If a rotten fruit gets mixed with unripe fruits, then the plant growth regulator – ethylene that is synthesized from the rotten fruits will speed up the process of ripening of the unripe fruits.
4. If you forget to add cytokinin to the culture medium, then the process of cell division, differentiation and growth will be dampened and get slower.