Question 2. 1. Fill in the blanks
(a) The volume of a cube of side 1 cm is equal to…………m3.
(b) The surface area of a solid cylinder of radius 2.0 cm and height 10.0 cm is equal to ……..(mm)2.
(c) A vehicle moving with a speed of 18 km h-1covers ………. m in 1 s.
(d) The relative density of lead is 11.3. Its density is …….. g cm-3or ………. kg m-3.
Answer:(a) Volume of cube, V = (1 cm)3= (10-2m)310-6m3.
Hence, answer is 10-6
(b) Surface area = 2πrh + 2πr2= 2πr (h + r)
= 2 x 22/7 x 2 x 10 (10 x 10 + 2 x 10) mm2= 1.5 x 104mm2Hence, answer is 1.5 x 104.
(c) Speed of vehicle = 18 km/h = 18 x 1000/3600 m/s
= 5 m/s ; so the vehicle covers 5 m in 1 s. = 11.3
(d) Density= 11.3 g cm-3
=11.3 x 103kg m-3[1 kg =103g,1m=102cm]
=11.3 x 103kg m-4
Question 2. 2. Fill in the blanks by suitable conversion of units
(a) 1 kg m2 s-2= …. g cm2s-2
(b) 1 m =………… ly
(c) 3.0 m s-2= …. kmh-2
(d) G = 6.67 x 10-11N m2(kg)-2= …. (cm)3s-2g-1.
Answer:

Question 2. 3. A calorie is a unit of heat or energy and it equals about 4.2 J where 1 J = 1 kgm2s-2. Suppose we employ a system of units in which the unit of mass equals a kg, the unit of length equals j8 m, the. unit of time is ys. Show that a calorie has a magnitude 4.2α-1 β-2 γ2in terms of the new units.
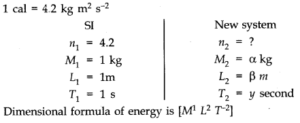
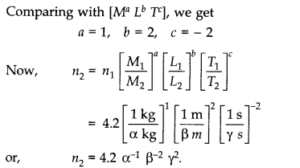
Question 2. 4. Explain this statement clearly:
“To call a dimensional quantity ‘large’ or ‘small’ is meaningless without specifying a standard for comparison”. In view of this, reframe the following statements wherever necessary:
(a) atoms are very small objects
(b) a jet plane moves with great speed
(c) the mass of Jupiter is very large
(d) the air inside this room contains a large number of molecules
(e) a proton is much more massive than an electron
(f) the speed of sound is much smaller than the speed of light.
Answer:Physical quantities are called large or small depending on the unit (standard) of measurement. For example, the distance between two cities on earth is measured in kilometres but the distance between stars or inter —galactic distances are measured in parsec. The later standard parsec is equal to 3.08 x 1016m or 3.08 x 1012km is certainly larger than metre or kilometre. Therefore, the inter-stellar or intergalactic distances are certainly larger than the distances between two cities on earth.
(a) The size of an atom is much smaller than even the sharp tip of a pin.
(b) A Jet plane moves with a speed greater than that of a super fast train.
(c) The mass of Jupiter is very large compared to that of the earth.
(d) The air inside this room contains more number of molecules than in one mole of air.
(e) This is a correct statement.
(f) This is a correct statement.
Question 2. 5. A new unit of length is chosen such that the speed of light in vacuum is unity. What is the distance between the Sun and the Earth in terms of the new unit if light takes 8 min and 20 s to cover this distance?
Answer:Distance between Sun and Earth
= Speed of light in vacuum x time taken by light to travel from Sim to Earth = 3 x 108m/ s x 8 min 20 s = 3 x 108m/s x 500 s = 500 x 3 x 108m.
In the new system, the speed of light in vacuum is unity. So, the new unit of length is 3 x 108m.
.•. distance between Sun and Earth = 500 new units.
Question 2. 6. Which of the following is the most precise device for measuring length:
(a) a vernier callipers with 20 divisions on the sliding scale.
(b) a screw gauge of pitch 1 mm and 100 divisions on the circular scale.
(c) an optical instrument that can measure length to within a wavelength of light?
Answer:(a) Least count of vernier callipers = 1/20 = 0.05 mm = 5 x 10-5m
(b) Least count of screw gauge =Pitch/No. of divisions on circular scale = 1 x 10-3/100 = 1 x 10-5m
(c) Least count of optical instrument = 6000 A (average wavelength of visible light as 6000 A) = 6 x 10-7mAs the least count of optical instrument is least, it is the most precise device out of three instruments given to us.
Question 2.7. A student measures the thickness of a human hair by looking at it through a microscope of magnification 100. He makes 20 observations and finds that the average width of the hair in the field of view of the microscope is 3.5 mm. What is the estimate on the thickness of hair?
Answer:As magnification, m =thickness of image of hair/ real thickness of hair = 100
and average width of the image of hair as seen by microscope = 3.5 mm
.•. Thickness of hair =3.5 mm/100 = 0.035 mm
Question 2. 8. Answer the following:
(a) You are given a thread and a metre scale. How will you estimate the diameter of the thread?
(b) A screw gauge has a pitch of 1.0 mm and 200 divisions on the circular scale. Do you think it is possible to increase the accuracy of the screw gauge arbitrarily by increasing the number of divisions on the circular scale?
(c) The mean diameter of a thin brass rod is to be measured by vernier callipers. Why is a set of 100 measurements of the diameter expected to yield a more reliable estimate than a set of 5 measurements only?
Answer:(a) Wrap the thread a number of times on a round pencil so as to form a coil having its turns touching each other closely. Measure the length of this coil, mode by the thread, with a metre scale. If n be the number of turns of the coil and l be the length of the coil, then the length occupied by each single turn i.e., the thickness of the thread = 1/n .
This is equal to the diameter of the thread.
(b) We know that least count = Pitch/number of divisions on circular scale When number of divisions on circular scale is increased, least count is decreased. Hence the accuracy is increased. However, this is only a theoretical idea.Practically speaking, increasing the number of ‘turns would create many difficulties.
As an example, the low resolution of the human eye would make observations difficult. The nearest divisions would not clearly be distinguished as separate. Moreover, it would be technically difficult to maintain uniformity of the pitch of the screw throughout its length.
(c) Due to random errors, a large number of observation will give a more reliable result than smaller number of observations. This is due to the fact that the probability (chance) of making a positive random error of a given magnitude is equal to that of making a negative random error of the same magnitude. Thus in a large number of observations, positive and negative errors are likely to cancel each other. Hence more reliable result can be obtained.
Question 2. 9. The photograph of a house occupies an area of 1.75 cm2on a 35 mm slide. The slide is projected on to a screen, and the area of the house on the screen is 1.55 m2. What is the linear magnification of the projector-screen arrangement?
Answer:Here area of the house on slide = 1.75 cm2= 1.75 x 10-4m2and area of the house of projector-screen = 1.55 m2
.•. Areal magnification =Area on screen/Area on slide = 1.55 m2/ 1.75 x 10-4m2= 8.857 x 103
.•. Linear magnification
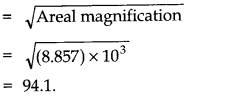
Question 2. 10. State the number of significant figures in the following:
(a) 0.007 m2(b) 2.64 x 104kg
(c) 0.2370 g cm-3(d) 6.320 J
(e) 6.032 N m-2(f) 0.0006032 m2
Answer:(a) 1 (b) 3 (c) 4 (d) 4 (e) 4 (f) 4.
Question 2 .11. ‘The length, breadth and thickness of a rectangular sheet of metal are 4.234 m, 1.005 m and 2.01 cm respectively. Give the area and volume of the sheet to correct significant figures.
Answer:As Area = (4.234 x 1.005) x 2 = 8.51034 = 8.5 m2
Volume = (4.234 x 1.005) x (2.01 x 10-2) = 8.55289 x 10-2= 0.0855 m3.
Question 2. 12. The mass of a box measured by a grocer’s balance is 2.3 kg. Two gold pieces of masses 20.15 g and 20.17 g are added to the box. What is (a) the total mass of the box (b) the difference in the masses of the pieces to correct significant figures?
Answer:(a) Total mass of the box = (2.3 + 0.0217 + 0.0215) kg = 2.3442 kg
Since the least number of decimal places is 1, therefore, the total mass of the box = 2.3 kg.
(b) Difference of mass = 2.17 – 2.15 = 0.02 g
Since the least number of decimal places is 2 so the difference in masses to the correct significant figures is 0.02 g.
Question 2. 13. A physical quantity P is related to four observables a, b, c and d as follows:
![]()
The percentage errors of measurement in a, b, c and d are 1%, 3%, 4% and 2%, respectively. What is the percentage error in the quantity P? If the value of P calculated using the above relation turns out to be 3.763, to what value should you round off the result?
Answer:

As the error lies in first decimal place, the answer should be rounded off to first decimal place. Hence, we shall express the value of P after rounding it off as P = 3.8.
Question 2. 14. A book with many printing errors contains four different formulas for the displacement y of a particle undergoing a certain periodic motion:
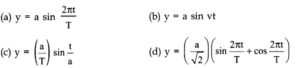
(a = maximum displacement of the particle, v = speed of the particle, T = time-period of motion)Rule out the wrong formulas on dimensional grounds.
Answer:According to dimensional analysis an equation must be dimensionally homogeneous.
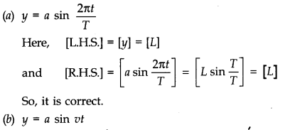

Question 2. 15. A famous relation in physics relates ‘moving mass’ m to the ‘rest mass’ m0 of a particle in terms of its speed v and the speed of light c. (This relation first arose as a consequence of special relativity due to Albert Einstein). A boy recalls the relation almost correctly but forgets where to put the constant c. He writes:

Guess where to put the missing c.
Answer:

Question 2. 16. The unit of length convenient on the atomic scale is known as an angstrom and is denoted by A: 1 A = 10-10m. The size of a hydrogen atom is about 0.5 A. What is the total atomic volume in m3of a mole of hydrogen atoms?
Answer:Volume of one hydrogen atom = 4/3 πr3 (volume of sphere)
= 4/3 x 3.14 x (0.5 x 10-10) m3= 5.23 x 10-31m3
According to Avagadro’s hypothesis, one mole of hydrogen contains 6.023 x 1023atoms.
Atomic volume of 1 mole of hydrogen atoms
= 6.023 x 1023 x 5.23 x 10-31= 3.15 x 10-7m3.
Question 2. 17. One mole of an ideal gas at standard temperature and pressure occupies 22.4 L (molar volume). What is the ratio of molar volume to the atomic volume of a mole of hydrogen? (Take the size of hydrogen molecule to be about 1 A.) Why is this ratio so large?
Answer:Volume of one mole of ideal gas, Vg
= 22.4 litre = 22.4 x 10-3m3
Radius of hydrogen molecule = 1A/2
= 0.5 A = 0.5 x 10-10m
Volume of hydrogen molecule = 4/3 πr3
=4/3 x 22/7 (0.5 x 10-10)3m3
= 0.5238 x 10-30m3
One mole contains 6.023 x 1023molecules.
Volume of one mole of hydrogen, VH
= 0.5238 x 10-30x 6.023 x 1023m3= 3.1548 x 10-7m3
Now Vg/VH=22.4 x 10-3/3.1548 x 10-7=7.1 x 104
The ratio is very large. This is because the interatomic separation in the gas is very large compared to the size of a hydrogen molecule.
Question 2. 18. Explain this common observation clearly: If you look out of the window of a fast moving train, the nearby trees, houses etc., seem to move rapidly in a direction opposite to the train’s motion, but the distant objects (hill tops, the Moon, the stars etc.) seem to be stationary. (In fact, since you are aware that you are moving, these distant objects seem to move with you).
Answer:The line joining a given object to our eye is known as the line of sight. When a train moves rapidly, the line of sight of a passenger sitting in the train for nearby trees changes its direction rapidly. As a result, the nearby trees and other objects appear to run in a direction opposite to the train’s motion. However, the line of sight of distant and large size objects e.g., hill tops, the Moon, the stars etc., almost remains unchanged (or changes by an extremely small angle). As a result, the distant object seems to be stationary.
Question 2. 19. The principle of ‘parallax’ is used in the determination of distances of very distant stars. The baseline AB is the line joining the Earth’s two locations six months apart in its orbit around the Sun. That is, the baseline is about the diameter of the Earth’s orbit =3 x 10 n m. However, even the nearest stars are so distant that with such a long baseline, they show parallel only of the order of 1″ (second) of arc or so. A parsec is a convenient unit of length on the astronomical scale. It is the distance of an object that will show a parallax of 1″ (second) of arc from opposite ends of a baseline equal to the distance from the Earth to the Sun. How much is a parsec in terms of metres?
Answer:From parallax method we can say
θ=b/D,where b=baseline ,D = distance of distant object or star
Since, θ=1″ (s) and b=3 x 1011m
D=b/20=3 x 1011/2 x 4.85 x 10-6m
or D=3 x 1011/9.7 x 10-6m =30 x 1016/9.7 m
= 3.09 x 1016m = 3 x 1016m.
Question 2. 20. The nearest star to our solar system is 4.29 light years away. How much is this distance in terms of parsecs? How much parallax would this star (named Alpha Centauri) show when viewed from two locations of the Earth six months apart in its orbit around the Sun?
Answer:As we know, 1 light year = 9.46 x 1015m
.•. 4.29 light years = 4.29 x 9.46 x 1015= 4.058 x 1016m
Also, 1 parsec = 3.08 x 1016m
.•. 4.29 light years =4.508 x 1016/3.80 x 1016= 1.318 parsec = 1.32 parsec.
As a parsec distance subtends a parallax angle of 1″ for a basis of radius of Earth’s orbit around the Sun (r).In present problem base is the distance between two locations of the Earth six months apart in its orbit around the Sun = diameter of Earth’s orbit (b = 2r).
.•. Parallax angle subtended by 1 parsec distance at this basis = 2 second (by definition of parsec).
.•. Parallax angle subtended by the star Alpha Centauri at the given basis θ = 1.32 x 2 = 2.64″.
Question 2. 21. Precise measurements of physical quantities are a need of science. For example, to ascertain the speed of an aircraft, one must have an accurate method to find its positions at closely separated instants of time. This was the actual motivation behind the discovery of radar in World War II. Think of different examples in modem science where precise measurements of length, time, mass etc., are needed. Also, wherever you can, give a quantitative idea of the precision needed.
Answer:Extremely precise measurements are needed in modem science. As an example, while launching a satellite using a space launch rocket system we must measure time to a precision of 1 micro second. Again working with lasers we require length measurements to an angstrom unit (1 A° = 10-10m) or even a fraction of it. For estimating nuclear sizes we require a precision of 10-15m. To measure atomic masses using mass spectrograph we require a precision of 10-30kg and so on.
Question 2.22. Just as precise measurements are necessary in science, it is equally important to be able to make rough estimates of quantities using rudimentary ideas and common observations. Think of ways by which you can estimate the following (where an estimate is difficult to obtain, try to get an upper bound on the quantity):
(a) the total mass of rain-bearing clouds over India during the Monsoon
(b) the mass of an elephant
(c) the wind speed during a storm
(d) the number of strands of hair on your head
(e) the number of air molecules in your classroom.
Answer:(a) The average rainfall of nearly 100 cm or 1 m is recorded by meteorologists, during Monsoon, in India. If A is the area of the country, then A = 3.3 million sq. km = 3.3 x 106(km)2 = 3.3 x 106x 106m2= 3.3 x 1012m2
Mass of rain-bearing clouds
= area x height x density = 3.3 x 1012x 1 x 1000 kg = 3.3 x 1015kg.
(b) Measure the depth of an empty boat in water. Let it be d1. If A be the base area of the boat, then volume of water displaced by boat, V1 = Ad2
Let d2 be the depth of boat in water when the elephant is moved into the boat. Volume of water displaced by (boat + elephant), V2 = Ad2 Volume of water displaced by elephant,
V = V2-V1 = A(d2 -d1)
If p be the density of water, then mass of elephant = mass of water displaced by it = A(d2 – d1) p.
(c) Wind speed can be estimated by floating a gas-filled balloon in air at a known height h. When there is no wind, the balloon is at A. Suppose the wind starts blowing to the right such that the balloon drifts to position B in 1 second. Now, AB = d = hθ.
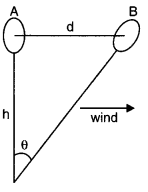
The value of d directly gives the wind speed.
(d) Let us assume that the man is not partially bald. Let us further assume that the hair on the head are uniformly distributed. We can estimate the area of the head. The thickness of a hair can be measured by using a screw gauge. The number of hair on the head is clearly the ratio of the area of head to the cross-sectional area of a hair.
Assume that the human head is a circle of radius 0.08 m i.e., 8 cm. Let us further assume that the thickness of a human air is 5 x 10-5m.
Number of hair on the head
=Area of the head/Area of cross – section of a hair
=π (0.08)2/π(5 x 10-5)=64 x 10-4/25 x 10-10=2.56 x 106
The number of hair on the human head is of the order of one million.
(e) We can determine the volume of the class-room by measuring its length, breadth and height. Consider a class room of size 10 m x 8 m x 4 m. Volume of this room is 320 m3. We know that 22.4l or 22.4 x 10-3m3of air has 6.02 x 1023molecules (equal to Avogadro’s number).
Number of molecules of air in the class room
=(6.02 x 1023/22.4 x 10-3) x 320 =8.6 x 1027
Question 2. 23. The Sun is a hot plasma (ionized matter) with its inner core at a temperature exceeding 107 K, and its outer surface at a temperature of about 6000 K. At these high temperatures, no substance remains in a solid or liquid phase. In what range do you expect the mass density of the Sun to be, in the range of densities of solids and liquids or gases? Check if your guess is correct from the following data: mass of the Sun = 2.0 x 1030kg, radius of the Sun = 7.0 x 108m.
Answer:Given M = 2 x 1030kg, r = 7 x 108m
.-. Volume of Sun = 4/3πr3x 3.14 x (7 x 108)3 = 1.437 x 1027m3
As p = M/V, .’. p = 2 x1030/1.437 x 1027= 1391.8 kg m-3= 1.4 x 103kg m-3
Mass density of Sun is in the range of mass densities of solids/liquids and not gases.
Question 2. 24. When the planet Jupiter is at a distance of 824.7 million kilometres from the Earth, its angular diameter is measured to be 35.72″ of arc. Calculate the diameter of Jupiter.
Answer:Given angular diameter θ = 35.72= 35.72 x 4.85 x 10-6rad
= 173.242 x 10-6= 1.73 x 10-4rad
Diameter of Jupiter D = θ x d = 1.73 x 10-4x 824.7 x 109m
=1426.731 x 103= 1.43 x 108m
Question 2. 25. A man walking briskly in rain with speed v must slant his umbrella forward making an angle θ with the vertical. A student derives the following relation between θ and v: tanθ = v and checks that the relation has a correct limit: as v—>θ, θ —>0, as expected. (We are assuming there is no strong wind and that the rain falls vertically for a stationary man). Do you think this relation can be correct? If not, guess the correct relation.
Answer:According to principle of homogenity of dimensional equations,
Dimensions of L.H.S. = Dimensions of R.H.S.
Here, v = tan θ
i. e., [L1T-1] = dimensionless, which is incorrect.
Correcting the L.H.S., we. get
v/u= tan θ, where u is velocity of rain.
Question 2. 26. It is claimed that two cesium clocks, if allowed to run for 180 years, free from any disturbance, may differ by only about 0.02 s. What does this imply for the accuracy of the standard cesium clock in measuring a time-interval of 1 s?
Answer:Total time = 100 years = 100 x 365 x 24 x 60 x 60 s
Error in 1 second=0.02/100 x 365 x 24 x 60 x 60
=6.34 x 10-12s
.•. Accuracy of 1 part in 1011to 1012.
Question 2. 27. Estimate the average mass density of a sodium atom assuming its size to be about
2.5 A. (Use the known values of Avogadro’s number and the atomic mass of sodium). Compare it with the density of sodium in its crystalline phase: 970 kg m3-. Are the two densities of the same order of magnitude? If so, why?
Answer:It is given that radius of sodium atom, R = 2.5 A = 2.5 x 10-10m
Volume of one mole atom of sodium, V = NA .4/3 π R3
V = 6.023 x 1023x –4/3 x 3.14 x (2.5 x 10-10)3m3and mass of one mole atom of sodium, M = 23 g = 23 x 10-3kg
.•. Average mass density of sodium atom, p = M/V
=(23 x 10-3/6.023 x 1023x 4/3 x 3.14 x (2.5 x 10-10))
= 6.96 x 102kg m-3= 0.7 x 10-3kg m-3
The density of sodium in its crystalline phase = 970 kg m-3
= 0.97 x 103kg m-3
Obviously the two densities are of the same order of magnitude (= 103kg m-3). It is on account of the fact that in solid phase atoms are tightly packed and so the atomic mass density is close to the mass density of solid.
Question 2. 28. The unit of length convenient on the nuclear scale is afermi: I f=10-15m. Nuclear sizes obey roughly the following empirical relation:
r = r0 A1/3
where r is the radius of the nucleus, A its mass number, and r0 is a constant equal to about,1.2 f. Show that the rule implies that nuclear mass density is nearly constant for different nuclei. Estimate the mass density of sodium nucleus. Compare it with the average mass density of a sodium atom obtained in Exercise 2.27.
Answer:Assume that the nucleus is spherical. Volume of nucleus
= 4/3 πr3= 4/3 π [r0A1/3]3= 4/3 πr03A
Mass of nucleus = A
.•. Nuclear mass density = Mass of nucleus/Volume of nucleus
= A/(4/3πr03A) = 3/4πr03
Since r0 is a constant therefore the right hand side is a constant. So, the nuclear mass density is independent of mass number. Thus, nuclear mass density is constant for different nuclei.
For sodium, A = 23
.’. radius of sodium nucleus,
r = 1.2 x 10-15(23)1/3m = 1.2 x 2.844 x 10-15m =3.4128 x 10-15

So, the nuclear mass density is nearly 50 million times more than the atomic mass density for a sodium atom.
Question 2. 29. A LASER is source of very intense, monochromatic, and unidirectional beam of light. These properties of a laser light can be exploited to measure long distances. The distance of the Moon from the Earth has been already determined very precisely using a laser as a source of light. A laser light beamed at the Moon takes 2.56 s to return after reflection at the Moon’s surface. How much is the radius of the lunar orbit around the Earth?
Answer:We known that speed of laser light = c = 3 x 108m/s. If d be the distance of Moon from the earth, the time taken by laser signal to return after reflection at the Moon’s surface
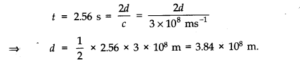
Question 2. 30. A SONAR (sound navigation and ranging) uses ultrasonic waves to detect and locate objects under water. In a submarine equipped with a SONAR the time delay between generation of a probe wave and the reception of its echo after reflection from an enemy submarine is found to be 77.0 s. What is the distance of the enemy submarine? (Speed of sound in water = 1450 m s-1).
Answer:Here speed of sound in water v = 1450 m s-1and time of echo t = 77.0 s.
If distance of enemy submarine be d, then t = 2d/v
.’. d=vt/2 =1450 x 77.0/2 =55825 m=55.8 x 103m or 55.8 km.
Question 2. 31. The farthest objects in our Universe discovered by modem astronomers are so distant that light emitted by them takes billions of years to reach the Earth. These objects (known as quasars) have many puzzling features, which have not yet been satisfactorily explained. What is the distance in km of a quasar from which light takes 3.0 billion years to reach us?
Answer:The time taken by light from the quasar to the observer
t = 3.0 billion years = 3.0 x 109years As 1 ly = 9.46 x 1015m
.•. Distance of quasar from the observer d = 3.0 x 109x 9.46 x 1015 m
= 28.38 x 1024m = 2.8 x 1025m or 2.8 x 1022km.
Question 2. 32. It is a well known fact that during a total solar eclipse the disk of the Moon almost completely covers the disk of the Sun. From this fact and from the information you can gather from examples 2.3 and 2.4, determine the approximate diameter of the Moon.
Answer:From examples 2.3 and 2.4, we get θ = 1920″ andS = 3.8452 x 108m. During the total solar eclipse, the disc of the moon completely covers the disc of the sun, so the angular diameter of both the sun and the moon must be equal. Angular diameter of the moon, θ= Angular diameter of the sun
= 1920″ = 1920 x 4.85 x10-6rad [1″ = 4.85 x 10-6rad]
The earth-moon distance, S = 3.8452 x 108m .’. The diameter of the moon, D = θ x S
= 1920 x 4.85 x 10-6x 3.8452 x 108m = 35806.5024 x 102m = 3581 x 103m 3581 km.
Question 2. 33. A great physicist of this century (P.A.M. Dirac) loved playing with numerical values of fundamental constants of nature. This led him to an interesting observation. Dirac found that from the basic constants of atomic physics (c, e, mass of electron, mass of proton) and the gravitational constant G, he could arrive at a number with the dimension of time. Further, it was a very large number, its magnitude being close to the present estimate on the age of the universe (-15 billion years). From the table of fundamental constants in this book, try to see if you too can construct this number (or any other interesting number you can think of). If its coincidence with the age of the universe were significant, what would this imply for the constancy of fundamental constants?
Answer:The values of different fundamental constants are given below:

We have to try to make permutations and combinations of the universal constants and see if there can be any such combination whose dimensions come out to be the dimensions of time. One such combination is:





