Chapter 5 - Arithmetic Progressions Questions and Answers: NCERT Solutions for Class 10 Mathematics

Exercise 5.1

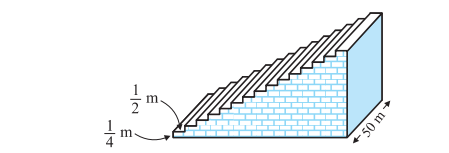
1. In which of the following situations, does the list of numbers involved make as arithmetic progression and why? (i) The taxi fare after each km when the fare is Rs 15 for the first km and Rs 8 for each additional km.

Solution: We can write the given condition as; Taxi fare for 1 km = 15 Taxi fare for first 2 kms = 15+8 = 23 Taxi fare for first 3 kms = 23+8 = 31 Taxi fare for first 4 kms = 31+8 = 39 And so on…… Thus, 15, 23, 31, 39 … forms an A.P. because every next term is 8 more than the preceding term.

(ii) The amount of air present in a cylinder when a vacuum pump removes 1/4 of the air remaining in the cylinder at a time.

Solution: Let the volume of air in a cylinder, initially, be V litres. In each stroke, the vacuum pump removes 1/4th of air remaining in the cylinder at a time. Or we can say, after every stroke, 1-1/4 = 3/4th part of air will remain. Therefore, volumes will be V, 3V/4 , (3V/4)2 , (3V/4)3…and so on Clearly, we can see here, the adjacent terms of this series do not have the common difference between them. Therefore, this series is not an A.P.

(iii) The cost of digging a well after every metre of digging, when it costs Rs 150 for the first metre and rises by Rs 50 for each subsequent metre.

Solution: We can write the given condition as; Cost of digging a well for first metre = Rs.150 Cost of digging a well for first 2 metres = Rs.150+50 = Rs.200 Cost of digging a well for first 3 metres = Rs.200+50 = Rs.250 Cost of digging a well for first 4 metres =Rs.250+50 = Rs.300 And so on.. Clearly, 150, 200, 250, 300 … forms an A.P. with a common difference of 50 between each term.

(iv) The amount of money in the account every year, when Rs 10000 is deposited at compound interest at 8% per annum.

Solution: We know that if Rs. P is deposited at r% compound interest per annum for n years, the amount of money will be: P(1+r/100)n Therefore, after each year, the amount of money will be; 10000(1+8/100), 10000(1+8/100)2, 10000(1+8/100)3…… Clearly, the terms of this series do not have the common difference between them. Therefore, this is not an A.P.

2. Write first four terms of the A.P. when the first term a and the common difference are given as follows: (i) a = 10, d = 10 (ii) a = -2, d = 0 (iii) a = 4, d = – 3 (iv) a = -1 d = 1/2 (v) a = – 1.25, d = – 0.25

Solutions: (i) a = 10, d = 10 Let us consider, the Arithmetic Progression series be a1, a2, a3, a4, a5 … a1 = a = 10 a2 = a1+d = 10+10 = 20 a3 = a2+d = 20+10 = 30 a4 = a3+d = 30+10 = 40 a5 = a4+d = 40+10 = 50 And so on… Therefore, the A.P. series will be 10, 20, 30, 40, 50 … And First four terms of this A.P. will be 10, 20, 30, and 40.

(ii) a = – 2, d = 0 Let us consider, the Arithmetic Progression series be a1, a2, a3, a4, a5 … a1 = a = -2 a2 = a1+d = – 2+0 = – 2 a3 = a2+d = – 2+0 = – 2 a4 = a3+d = – 2+0 = – 2 Therefore, the A.P. series will be – 2, – 2, – 2, – 2 … And, First four terms of this A.P. will be – 2, – 2, – 2 and – 2.

(iii) a = 4, d = – 3 Let us consider, the Arithmetic Progression series be a1, a2, a3, a4, a5 … a1 = a = 4 a2 = a1+d = 4-3 = 1 a3 = a2+d = 1-3 = – 2 a4 = a3+d = -2-3 = – 5 Therefore, the A.P. series will be 4, 1, – 2 – 5 … And, first four terms of this A.P. will be 4, 1, – 2 and – 5.

(iv) a = – 1, d = 1/2 Let us consider, the Arithmetic Progression series be a1, a2, a3, a4, a5 … a2 = a1+d = -1+1/2 = -1/2 a3 = a2+d = -1/2+1/2 = 0 a4 = a3+d = 0+1/2 = 1/2 Thus, the A.P. series will be-1, -1/2, 0, 1/2 And First four terms of this A.P. will be -1, -1/2, 0 and 1/2.

(v) a = – 1.25, d = – 0.25 Let us consider, the Arithmetic Progression series be a1, a2, a3, a4, a5 … a1 = a = – 1.25 a2 = a1 + d = – 1.25-0.25 = – 1.50 a3 = a2 + d = – 1.50-0.25 = – 1.75 a4 = a3 + d = – 1.75-0.25 = – 2.00 Therefore, the A.P series will be 1.25, – 1.50, – 1.75, – 2.00 …….. And first four terms of this A.P. will be – 1.25, – 1.50, – 1.75 and – 2.00.

3. For the following A.P.s, write the first term and the common difference. (i) 3, 1, – 1, – 3 … (ii) -5, – 1, 3, 7 … (iii) 1/3, 5/3, 9/3, 13/3 …. (iv) 0.6, 1.7, 2.8, 3.9 …

Solutions (i) Given series, 3, 1, – 1, – 3 … First term, a = 3 Common difference, d = Second term – First term ⇒  1 – 3 = -2 ⇒  d = -2

(ii) Given series, – 5, – 1, 3, 7 … First term, a = -5 Common difference, d = Second term – First term ⇒ ( – 1)-( – 5) = – 1+5 = 4

(iii) Given series, 1/3, 5/3, 9/3, 13/3 …. First term, a = 1/3 Common difference, d = Second term – First term ⇒ 5/3 – 1/3 = 4/3

(iv) Given series, 0.6, 1.7, 2.8, 3.9 … First term, a = 0.6 Common difference, d = Second term – First term ⇒ 1.7 – 0.6 ⇒ 1.1

4. Which of the following are APs? If they form an A.P. find the common difference d and write three more terms. (i) 2, 4, 8, 16 … (ii) 2, 5/2, 3, 7/2 …. (iii) -1.2, -3.2, -5.2, -7.2 … (iv) -10, – 6, – 2, 2 … (v) 3, 3 + √2, 3 + 2√2, 3 + 3√2 (vi) 0.2, 0.22, 0.222, 0.2222 …. (vii) 0, – 4, – 8, – 12 … (viii) -1/2, -1/2, -1/2, -1/2 …. (ix) 1, 3, 9, 27 … (x) a, 2a, 3a, 4a … (xi) a, a2, a3, a4 … (xii) √2, √8, √18, √32 … (xiii) √3, √6, √9, √12 … (xiv) 12, 32, 52, 72 … (xv) 12, 52, 72, 73 …

Solution (i) Given to us, 2, 4, 8, 16 … Here, the common difference is; a2 – a1 = 4 – 2 = 2 a3 – a2 = 8 – 4 = 4 a4 – a3 = 16 – 8 = 8 Since, an+1 – an or the common difference is not the same every time. Therefore, the given series are not forming an A.P.

(ii) Given, 2, 5/2, 3, 7/2 …. Here, a2 – a1 = 5/2-2 = 1/2 a3 – a2 = 3-5/2 = 1/2 a4 – a3 = 7/2-3 = 1/2 Since, an+1 – an or the common difference is same every time. Therefore, d = 1/2 and the given series are in A.P. The next three terms are; a5 = 7/2+1/2 = 4 a6 = 4 +1/2 = 9/2 a7 = 9/2 +1/2 = 5

(iii) Given, -1.2, – 3.2, -5.2, -7.2 … Here, a2 – a1 = (-3.2)-(-1.2) = -2 a3 – a2 = (-5.2)-(-3.2) = -2 a4 – a3 = (-7.2)-(-5.2) = -2 Since, an+1 – an or common difference is same every time. Therefore, d = -2 and the given series are in A.P. Hence, next three terms are; a5 = – 7.2-2 = -9.2 a6 = – 9.2-2 = – 11.2 a7 = – 11.2-2 = – 13.2

(iv) Given, -10, – 6, – 2, 2 …

Here, the terms and their difference are; a2 – a1 = (-6)-(-10) = 4 a3 – a2 = (-2)-(-6) = 4 a4 – a3 = (2 -(-2) = 4 Since, an+1 – an or the common difference is same every time. Therefore, d = 4 and the given numbers are in A.P. Hence, next three terms are; a5 = 2+4 = 6 a6 = 6+4 = 10 a7 = 10+4 = 14

(v) Given, 3, 3+√2, 3+2√2, 3+3√2

Here, a2 – a1 = 3+√2-3 = √2 a3 – a2 = (3+2√2)-(3+√2) = √2 a4 – a3 = (3+3√2) – (3+2√2) = √2 Since, an+1 – an or the common difference is same every time. Therefore, d = √2 and the given series forms a A.P. Hence, next three terms are; a5 = (3+√2) +√2 = 3+4√2 a6 = (3+4√2)+√2 = 3+5√2 a7 = (3+5√2)+√2 = 3+6√2 (vi) 0.2, 0.22, 0.222, 0.2222 ….

Here, a2 – a1 = 0.22-0.2 = 0.02 a3 – a2 = 0.222-0.22 = 0.002 a4 – a3 = 0.2222-0.222 = 0.0002 Since, an+1 – an or the common difference is not same every time. Therefore, and the given series doesn’t forms a A.P.

(vii) 0, -4, -8, -12 …

Here, a2 – a1 = (-4)-0 = -4 a3 – a2 = (-8)-(-4) = -4 a4 – a3 = (-12)-(-8) = -4 Since, an+1 – an or the common difference is same every time. Therefore, d = -4 and the given series forms a A.P. Hence, next three terms are; a5 = -12-4 = -16 a6 = -16-4 = -20 a7 = -20-4 = -24

(viii) -1/2, -1/2, -1/2, -1/2 ….

Here, a2 – a1 = (-1/2) – (-1/2) = 0 a3 – a2 = (-1/2) – (-1/2) = 0 a4 – a3 = (-1/2) – (-1/2) = 0 Since, an+1 – an or the common difference is same every time. Therefore, d = 0 and the given series forms a A.P. Hence, next three terms are; a5 = (-1/2)-0 = -1/2 a6 = (-1/2)-0 = -1/2 a7 = (-1/2)-0 = -1/2

(ix) 1, 3, 9, 27 …

Here, a2 – a1 = 3-1 = 2 a3 – a2 = 9-3 = 6 a4 – a3 = 27-9 = 18 Since, an+1 – an or the common difference is not same every time. Therefore, and the given series doesn’t form a A.P.

(x) a, 2a, 3a, 4a … Here, a2 – a1 = 2a–a = a a3 – a2 = 3a-2a = a a4 – a3 = 4a-3a = a Since, an+1 – an or the common difference is same every time. Therefore, d = a and the given series forms a A.P. Hence, next three terms are; a5 = 4a+a = 5a a6 = 5a+a = 6a a7 = 6a+a = 7a

(xi) a, a2, a3, a4 … Here, a2 – a1 = a2–a = a(a-1) a3 – a2 = a3 – a2 = a2(a-1) a4 – a3 = a4 – a3 = a3(a-1) Since, an+1 – an or the common difference is not same every time. Therefore, the given series doesn’t forms a A.P.

(xii) √2, √8, √18, √32 …

Here, a2 – a1 = √8-√2  = 2√2-√2 = √2 a3 – a2 = √18-√8 = 3√2-2√2 = √2 a4 – a3 = 4√2-3√2 = √2 Since, an+1 – an or the common difference is same every time. Therefore, d = √2 and the given series forms a A.P. Hence, next three terms are; a5 = √32+√2 = 4√2+√2 = 5√2 = √50 a6 = 5√2+√2 = 6√2 = √72 a7 = 6√2+√2 = 7√2 = √98

(xiii) √3, √6, √9, √12 … Here, a2 – a1 = √6-√3 = √3×√2-√3 = √3(√2-1) a3 – a2 = √9-√6 = 3-√6 = √3(√3-√2) a4 – a3 = √12 – √9 = 2√3 – √3×√3 = √3(2-√3) Since, an+1 – an or the common difference is not same every time. Therefore, the given series doesn’t form a A.P.

(xiv) 12, 32, 52, 72 … Or, 1, 9, 25, 49 ….. Here, a2 − a1 = 9−1 = 8 a3 − a2 = 25−9 = 16 a4 − a3 = 49−25 = 24 Since, an+1 – an or the common difference is not same every time. Therefore, the given series doesn’t form a A.P.

(xv) 12, 52, 72, 73 … Or 1, 25, 49, 73 … Here, a2 − a1 = 25−1 = 24 a3 − a2 = 49−25 = 24 a4 − a3 = 73−49 = 24 Since, an+1 – an or the common difference is same every time. Therefore, d = 24 and the given series forms a A.P. Hence, next three terms are; a5 = 73+24 = 97 a6 = 97+24 = 121 a7 = 121+24 = 145

Exercise 5.2

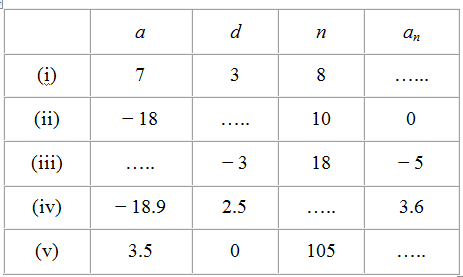
1. Fill in the blanks in the following table, given that a is the first term, d the common difference and an the nth term of the A.P.

Solutions: (i) Given, First term, a = 7 Common difference, d = 3 Number of terms, n = 8, We have to find the nth term, an = ? As we know, for an A.P., an = a+(n−1)d Putting the values, => 7+(8 −1) 3 => 7+(7) 3 => 7+21 = 28 Hence, an = 28

(ii) Given, First term, a = -18 Common difference, d = ? Number of terms, n = 10 Nth term, an = 0 As we know, for an A.P., an = a+(n−1)d Putting the values, 0 = − 18 +(10−1)d 18 = 9d d = 18/9 = 2 Hence, common difference, d = 2

(iii) Given, First term, a = ? Common difference, d = -3 Number of terms, n = 18 Nth term, an = -5 As we know, for an A.P., an = a+(n−1)d Putting the values, −5 = a+(18−1) (−3) −5 = a+(17) (−3) −5 = a−51 a = 51−5 = 46 Hence, a = 46

(iv) Given, First term, a = -18.9 Common difference, d = 2.5 Number of terms, n = ? Nth term, an = 3.6 As we know, for an A.P., an = a +(n −1)d Putting the values, 3.6 = − 18.9+(n −1)2.5 3.6 + 18.9 = (n−1)2.5 22.5 = (n−1)2.5 (n – 1) = 22.5/2.5 n – 1 = 9 n = 10 Hence, n = 10

(v) Given, First term, a = 3.5 Common difference, d = 0 Number of terms, n = 105 Nth term, an = ? As we know, for an A.P., an = a+(n −1)d Putting the values, an = 3.5+(105−1) 0 an = 3.5+104×0 an = 3.5 Hence, an = 3.5

2. Choose the correct choice in the following and justify: (i) 30th term of the A.P: 10,7, 4, …, is (A) 97 (B) 77 (C) −77 (D) −87 (ii) 11th term of the A.P. -3, -1/2, ,2 …. is (A) 28 (B) 22 (C) – 38 (D)

Solutions: (i) Given here, A.P. = 10, 7, 4, … Therefore, we can find, First term, a = 10 Common difference, d = a2 − a1 = 7−10 = −3 As we know, for an A.P., an = a +(n−1)d Putting the values; a30 = 10+(30−1)(−3) a30 = 10+(29)(−3) a30 = 10−87 = −77 Hence, the correct answer is option C.

(ii) Given here, A.P. = -3, -1/2, ,2 … Therefore, we can find, First term a = – 3 Common difference, d = a2 − a1 = (-1/2) -(-3) ⇒(-1/2) + 3 = 5/2 As we know, for an A.P., an = a+(n−1)d Putting the values; a11 = -3+(11-1)(5/2) a11 = -3+(10)(5/2) a11 = -3+25 a11 = 22 Hence, the answer is option B.

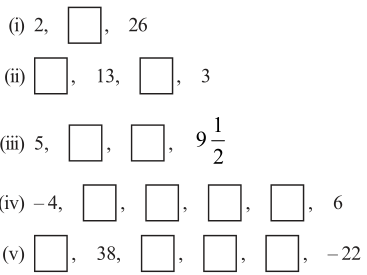
3. In the following APs find the missing term in the boxes.

Solutions: (i) For the given A.P., 2,2 , 26 The first and third term are; a = 2 a3 = 26 As we know, for an A.P., an = a+(n −1)d Therefore, putting the values here, a3 = 2+(3-1)d 26 = 2+2d 24 = 2d d = 12 a2 = 2+(2-1)12 = 14 Therefore, 14 is the missing term.

(ii) For the given A.P., , 13, ,3 a2 = 13 and a4 = 3 As we know, for an A.P., an = a+(n−1) d Therefore, putting the values here, a2 = a +(2-1)d 13 = a+d ………………. (i) a4 = a+(4-1)d 3 = a+3d ………….. (ii) On subtracting equation (i) from (ii), we get, – 10 = 2d d = – 5 From equation (i), putting the value of d,we get 13 = a+(-5) a = 18 a3 = 18+(3-1)(-5) = 18+2(-5) = 18-10 = 8 Therefore, the missing terms are 18 and 8 respectively.

(iii) For the given A.P., a = 5 and a4 = 19/2 As we know, for an A.P., an = a+(n−1)d Therefore, putting the values here, a4 = a+(4-1)d 19/2 = 5+3d (19/2) – 5 = 3d 3d = 9/2 d = 3/2 a2 = a+(2-1)d a2 = 5+3/2 a2 = 13/2 a3 = a+(3-1)d a3 = 5+2×3/2 a3 = 8 Therefore, the missing terms are 13/2 and 8 respectively.

(iv) For the given A.P., a = −4 and a6 = 6 As we know, for an A.P., an = a +(n−1) d Therefore, putting the values here, a6 = a+(6−1)d 6 = − 4+5d 10 = 5d d = 2 a2 = a+d = − 4+2 = −2 a3 = a+2d = − 4+2(2) = 0 a4 = a+3d = − 4+ 3(2) = 2 a5 = a+4d = − 4+4(2) = 4 Therefore, the missing terms are −2, 0, 2, and 4 respectively.

(v) For the given A.P., a2 = 38 a6 = −22 As we know, for an A.P., an = a+(n −1)d Therefore, putting the values here, a2 = a+(2−1)d 38 = a+d ……………………. (i) a6 = a+(6−1)d −22 = a+5d …………………. (ii) On subtracting equation (i) from (ii), we get − 22 − 38 = 4d −60 = 4d d = −15 a = a2 − d = 38 − (−15) = 53 a3 = a + 2d = 53 + 2 (−15) = 23 a4 = a + 3d = 53 + 3 (−15) = 8 a5 = a + 4d = 53 + 4 (−15) = −7 Therefore, the missing terms are 53, 23, 8, and −7 respectively.

4. Which term of the A.P. 3, 8, 13, 18, … is 78?

Solutions: Given the A.P. series as3, 8, 13, 18, … First term, a = 3 Common difference, d = a2 − a1 = 8 − 3 = 5 Let the nth term of given A.P. be 78. Now as we know, an = a+(n−1)d Therefore, 78 = 3+(n −1)5 75 = (n−1)5 (n−1) = 15 n = 16 Hence, 16th term of this A.P. is 78.

5. Find the number of terms in each of the following A.P. (i) 7, 13, 19, …, 205

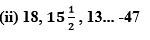
Solutions: (i) Given, 7, 13, 19, …, 205 is the A.P Therefore First term, a = 7 Common difference, d = a2 − a1 = 13 − 7 = 6 Let there are n terms in this A.P. an = 205 As we know, for an A.P., an = a + (n − 1) d Therefore, 205 = 7 + (n − 1) 6 198 = (n − 1) 6 33 = (n − 1) n = 34 Therefore, this given series has 34 terms in it.

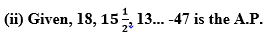
First term, a = 18 Common difference, d = a2-a1 =

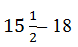
d = (31-36)/2 = -5/2 Let there are n terms in this A.P. an = -47 As we know, for an A.P., an = a+(n−1)d -47 = 18+(n-1)(-5/2) -47-18 = (n-1)(-5/2) -65 = (n-1)(-5/2) (n-1) = -130/-5 (n-1) = 26 n = 27 Therefore, this given A.P. has 27 terms in it.

6. Check whether -150 is a term of the A.P. 11, 8, 5, 2, …

Solution: For the given series, A.P. 11, 8, 5, 2.. First term, a = 11 Common difference, d = a2−a1 = 8−11 = −3 Let −150 be the nth term of this A.P. As we know, for an A.P., an = a+(n−1)d -150 = 11+(n -1)(-3) -150 = 11-3n +3 -164 = -3n n = 164/3 Clearly, n is not an integer but a fraction. Therefore, – 150 is not a term of this A.P.

7. Find the 31st term of an A.P. whose 11th term is 38 and the 16th term is 73.

Solution: Given that, 11th term, a11 = 38 and 16th term, a16 = 73 We know that, an = a+(n−1)d a11 = a+(11−1)d 38 = a+10d ………………………………. (i) In the same way, a16 = a +(16−1)d 73 = a+15d ………………………………………… (ii) On subtracting equation (i) from (ii), we get 35 = 5d d = 7 From equation (i), we can write, 38 = a+10×(7) 38 − 70 = a a = −32 a31 = a +(31−1) d = − 32 + 30 (7) = − 32 + 210 = 178 Hence, 31st term is 178.

8. An A.P. consists of 50 terms of which 3rd term is 12 and the last term is 106. Find the 29th term.

Solution: Given that, 3rd term, a3 = 12 50th term, a50 = 106 We know that, an = a+(n−1)d a3 = a+(3−1)d 12 = a+2d ……………………………. (i) In the same way, a50 = a+(50−1)d 106 = a+49d …………………………. (ii) On subtracting equation (i) from (ii), we get 94 = 47d d = 2 = common difference From equation (i), we can write now, 12 = a+2(2) a = 12−4 = 8 a29 = a+(29−1) d a29 = 8+(28)2 a29 = 8+56 = 64 Therefore, 29th term is 64.

9. If the 3rd and the 9th terms of an A.P. are 4 and − 8 respectively. Which term of this A.P. is zero.

Solution: Given that, 3rd term, a3 = 4 and 9th term, a9 = −8 We know that, an = a+(n−1)d Therefore, a3 = a+(3−1)d 4 = a+2d ……………………………………… (i) a9 = a+(9−1)d −8 = a+8d ………………………………………………… (ii) On subtracting equation (i) from (ii), we will get here, −12 = 6d d = −2 From equation (i), we can write, 4 = a+2(−2) 4 = a−4 a = 8 Let nth term of this A.P. be zero. an = a+(n−1)d 0 = 8+(n−1)(−2) 0 = 8−2n+2 2n = 10 n = 5 Hence, 5th term of this A.P. is 0.

10. If 17th term of an A.P. exceeds its 10th term by 7. Find the common difference.

Solution: We know that, for an A.P series; an = a+(n−1)d a17 = a+(17−1)d a17 = a +16d In the same way, a10 = a+9d As it is given in the question, a17 − a10 = 7 Therefore, (a +16d)−(a+9d) = 7 7d = 7 d = 1 Therefore, the common difference is 1.

11. Which term of the A.P. 3, 15, 27, 39,.. will be 132 more than its 54th term?

Solution: Given A.P. is 3, 15, 27, 39, … first term, a = 3 common difference, d = a2 − a1 = 15 − 3 = 12 We know that, an = a+(n−1)d Therefore, a54 = a+(54−1)d ⇒3+(53)(12) ⇒3+636 = 639 a54 = 639+132=771 We have to find the term of this A.P. which is 132 more than a54, i.e.771. Let nth term be 771. an = a+(n−1)d 771 = 3+(n −1)12 768 = (n−1)12 (n −1) = 64 n = 65 Therefore, 65th term was 132 more than 54th term. Or another method is;

Let nth term be 132 more than 54th term. n = 54 + 132/2 = 54 + 11 = 65th term

12. Two APs have the same common difference. The difference between their 100th term is 100, what is the difference between their 1000th terms?

Solution: Let, the first term of two APs be a1 and a2 respectively And the common difference of these APs be d. For the first A.P.,we know, an = a+(n−1)d Therefore, a100 = a1+(100−1)d = a1 + 99d a1000 = a1+(1000−1)d a1000 = a1+999d For second A.P., we know, an = a+(n−1)d Therefore, a100 = a2+(100−1)d = a2+99d a1000 = a2+(1000−1)d = a2+999d Given that, difference between 100th term of the two APs = 100 Therefore, (a1+99d) − (a2+99d) = 100 a1−a2 = 100……………………………………………………………….. (i) Difference between 1000th terms of the two APs (a1+999d) − (a2+999d) = a1−a2 From equation (i), This difference, a1−a2 = 100 Hence, the difference between 1000th terms of the two A.P. will be 100.

13. How many three digit numbers are divisible by 7?

Solution: First three-digit number that is divisible by 7 are; First number = 105 Second number = 105+7 = 112 Third number = 112+7 =119 Therefore, 105, 112, 119, … All are three digit numbers are divisible by 7 and thus, all these are terms of an A.P. having first term as 105 and common difference as 7. As we know, the largest possible three-digit number is 999. When we divide 999 by 7, the remainder will be 5. Therefore, 999-5 = 994 is the maximum possible three-digit number that is divisible by 7. Now the series is as follows. 105, 112, 119, …, 994 Let 994 be the nth term of this A.P. first term, a = 105 common difference, d = 7 an = 994 n = ? As we know, an = a+(n−1)d 994 = 105+(n−1)7 889 = (n−1)7 (n−1) = 127 n = 128 Therefore, 128 three-digit numbers are divisible by 7.

14. How many multiples of 4 lie between 10 and 250?

Solution: The first multiple of 4 that is greater than 10 is 12. Next multiple will be 16. Therefore, the series formed as; 12, 16, 20, 24, … All these are divisible by 4 and thus, all these are terms of an A.P. with first term as 12 and common difference as 4. When we divide 250 by 4, the remainder will be 2. Therefore, 250 − 2 = 248 is divisible by 4. The series is as follows, now; 12, 16, 20, 24, …, 248 Let 248 be the nth term of this A.P. first term, a = 12 common difference, d = 4 an = 248 As we know, an = a+(n−1)d 248 = 12+(n-1)×4 236/4 = n-1 59  = n-1 n = 60 Therefore, there are 60 multiples of 4 between 10 and 250.

15. For what value of n, are the nth terms of two APs 63, 65, 67, and 3, 10, 17, … equal?

Solution: Given two APs as; 63, 65, 67,… and 3, 10, 17,…. Taking first AP, 63, 65, 67, … First term, a = 63 Common difference, d = a2−a1 = 65−63 = 2 We know, nth term of this A.P. = an = a+(n−1)d an= 63+(n−1)2 = 63+2n−2 an = 61+2n ………………………………………. (i) Taking second AP, 3, 10, 17, … First term, a = 3 Common difference, d = a2 − a1 = 10 − 3 = 7 We know that, nth term of this A.P. = 3+(n−1)7 an = 3+7n−7 an = 7n−4 ……………………………………………………….. (ii) Given, nth term of these A.P.s are equal to each other. Equating both these equations, we get, 61+2n = 7n−4 61+4 = 5n 5n = 65 n = 13 Therefore, 13th terms of both these A.P.s are equal to each other.

16. Determine the A.P. whose third term is 16 and the 7th term exceeds the 5th term by 12.

Solutions: Given, Third term, a3 = 16 As we know, a +(3−1)d = 16 a+2d = 16 ………………………………………. (i) It is given that, 7th term exceeds the 5th term by 12. a7 − a5 = 12 [a+(7−1)d]−[a +(5−1)d]= 12 (a+6d)−(a+4d) = 12 2d = 12 d = 6 From equation (i), we get, a+2(6) = 16 a+12 = 16 a = 4 Therefore, A.P. will be4, 10, 16, 22, …

17. Find the 20th term from the last term of the A.P. 3, 8, 13, …, 253.

Solution: Given A.P. is3, 8, 13, …, 253 Common difference, d= 5. Therefore, we can write the given AP in reverse order as; 253, 248, 243, …, 13, 8, 5 Now for the new AP, first term, a = 253 and common difference, d = 248 − 253 = −5 n = 20 Therefore, using nth term formula, we get, a20 = a+(20−1)d a20 = 253+(19)(−5) a20 = 253−95 a = 158 Therefore, 20th term from the last term of the AP 3, 8, 13, …, 253.is 158.

18. The sum of 4th and 8th terms of an A.P. is 24 and the sum of the 6th and 10th terms is 44. Find the first three terms of the A.P.

Solution: We know that, the nth term of the AP is; an = a+(n−1)d a4 = a+(4−1)d a4 = a+3d In the same way, we can write, a8 = a+7d a6 = a+5d a10 = a+9d Given that, a4+a8 = 24 a+3d+a+7d = 24 2a+10d = 24 a+5d = 12 …………………………………………………… (i) a6+a10 = 44 a +5d+a+9d = 44 2a+14d = 44 a+7d = 22 …………………………………….. (ii) On subtracting equation (i) from (ii), we get, 2d = 22 − 12 2d = 10 d = 5 From equation (i), we get, a+5d = 12 a+5(5) = 12 a+25 = 12 a = −13 a2 = a+d = − 13+5 = −8 a3 = a2+d = − 8+5 = −3 Therefore, the first three terms of this A.P. are −13, −8, and −3.

19. Subba Rao started work in 1995 at an annual salary of Rs 5000 and received an increment of Rs 200 each year. In which year did his income reach Rs 7000?

Solution: It can be seen from the given question, that the incomes of Subba Rao increases every year by Rs.200 and hence, forms an AP. Therefore, after 1995, the salaries of each year are; 5000, 5200, 5400, … Here, first term, a = 5000 and common difference, d = 200 Let after nth year, his salary be Rs 7000. Therefore, by the nth term formula of AP, an = a+(n−1) d 7000 = 5000+(n−1)200 200(n−1)= 2000 (n−1) = 10 n = 11 Therefore, in 11th year, his salary will be Rs 7000.

20. Ramkali saved Rs 5 in the first week of a year and then increased her weekly saving by Rs 1.75. If in the nth week, her weekly savings become Rs 20.75, find n.

Solution: Given that, Ramkali saved Rs.5 in first week and then started saving each week by Rs.1.75. Hence, First term, a = 5 and common difference, d = 1.75 Also given, an = 20.75 Find, n = ? As we know, by the nth term formula, an = a+(n−1)d Therefore, 20.75 = 5+(n -1)×1.75 15.75 = (n -1)×1.75 (n -1) = 15.75/1.75 = 1575/175 = 63/7 = 9 n -1 = 9 n = 10 Hence, n is 10.

Exercise 5.3

1. Find the sum of the following APs. (i) 2, 7, 12 ,…., to 10 terms. (ii) − 37, − 33, − 29 ,…, to 12 terms (iii) 0.6, 1.7, 2.8 ,…….., to 100 terms (iv) 1/15, 1/12, 1/10, …… , to 11 terms

Solutions: (i) Given, 2, 7, 12 ,…, to 10 terms For this A.P., first term, a = 2 And common difference, d = a2 − a1 = 7−2 = 5 n = 10 We know that, the formula for sum of nth term in AP series is, Sn = n/2 [2a +(n-1)d] S10 = 10/2 [2(2)+(10 -1)×5] = 5[4+(9)×(5)] = 5 × 49 = 245

(ii) Given, −37, −33, −29 ,…, to 12 terms For this A.P., first term, a = −37 And common difference, d = a2− a1 d= (−33)−(−37) = − 33 + 37 = 4 n = 12 We know that, the formula for sum of nth term in AP series is, Sn = n/2 [2a+(n-1)d] S12 = 12/2 [2(-37)+(12-1)×4] = 6[-74+11×4] = 6[-74+44] = 6(-30) = -180

(iii) Given, 0.6, 1.7, 2.8 ,…, to 100 terms For this A.P., first term, a = 0.6 Common difference, d = a2 − a1 = 1.7 − 0.6 = 1.1 n = 100 We know that, the formula for sum of nth term in AP series is, Sn = n/2[2a +(n-1)d] S12 = 50/2 [1.2+(99)×1.1] = 50[1.2+108.9] = 50[110.1] = 5505

(iv) Given, 1/15, 1/12, 1/10, …… , to 11 terms For this A.P., First term, a = 1/5 Common difference, d = a2 –a1 = (1/12)-(1/5) = 1/60 And number of terms n = 11 We know that, the formula for sum of nth term in AP series is, Sn = n/2 [2a + (n – 1) d]

= 11/2(2/15 + 10/60) = 11/2 (9/30) = 33/20

2. Find the sums given below:

(ii) 34 + 32 + 30 + ……….. + 10 (iii) − 5 + (− 8) + (− 11) + ………… + (− 230)

Solutions: (i)

First term, a = 7 nth term, an = 84

Let 84 be the nth term of this A.P., then as per the nth term formula, an = a(n-1)d 84 = 7+(n – 1)×7/2 77 = (n-1)×7/2 22 = n−1 n = 23 We know that, sum of n term is; Sn = n/2 (a + l) , l = 84 Sn = 23/2 (7+84) Sn  = (23×91/2) = 2093/2

(ii) Given, 34 + 32 + 30 + ……….. + 10 For this A.P., first term, a = 34 common difference, d = a2−a1 = 32−34 = −2 nth term, an= 10 Let 10 be the nth term of this A.P., therefore, an= a +(n−1)d 10 = 34+(n−1)(−2) −24 = (n −1)(−2) 12 = n −1 n = 13 We know that, sum of n terms is; Sn = n/2 (a +l) , l = 10 = 13/2 (34 + 10) = (13×44/2) = 13 × 22 = 286

(iii) Given, (−5) + (−8) + (−11) + ………… + (−230) For this A.P., First term, a = −5 nth term, an= −230 Common difference, d = a2−a1 = (−8)−(−5) ⇒d = − 8+5 = −3 Let −230 be the nth term of this A.P., and by the nth term formula we know, an= a+(n−1)d −230 = − 5+(n−1)(−3) −225 = (n−1)(−3) (n−1) = 75 n = 76 And, Sum of n term, Sn = n/2 (a + l) = 76/2 [(-5) + (-230)] = 38(-235) = -8930

3. In an AP (i) Given a = 5, d = 3, an = 50, find n and Sn. (ii) Given a = 7, a13 = 35, find d and S13. (iii) Given a12 = 37, d = 3, find a and S12. (iv) Given a3 = 15, S10 = 125, find d and a10. (v) Given d = 5, S9 = 75, find a and a9. (vi) Given a = 2, d = 8, Sn = 90, find n and an. (vii) Given a = 8, an = 62, Sn = 210, find n and d. (viii) Given an = 4, d = 2, Sn = − 14, find n and a. (ix) Given a = 3, n = 8, S = 192, find d. (x) Given l = 28, S = 144 and there are total 9 terms. Find a.

Solutions: (i) Given that, a = 5, d = 3, an = 50 As we know, from the formula of the nth term in an AP, an = a +(n −1)d, Therefore, putting the given values, we get, ⇒ 50 = 5+(n -1)×3 ⇒ 3(n -1) = 45 ⇒ n -1 = 15 ⇒ n = 16 Now, sum of n terms, Sn = n/2 (a +an) Sn = 16/2 (5 + 50) = 440

(ii) Given that, a = 7, a13 = 35 As we know, from the formula of the nth term in an AP, an = a+(n−1)d, Therefore, putting the given values, we get, ⇒ 35 = 7+(13-1)d ⇒ 12d = 28 ⇒ d = 28/12 = 2.33 Now, Sn = n/2 (a+an) S13 = 13/2 (7+35) = 273

(iii) Given that, a12 = 37, d = 3 As we know, from the formula of the nth term in an AP, an = a+(n −1)d, Therefore, putting the given values, we get, ⇒ a12 = a+(12−1)3 ⇒ 37 = a+33 ⇒ a = 4 Now, sum of nth term, Sn = n/2 (a+an) Sn = 12/2 (4+37) = 246

(iv) Given that, a3 = 15, S10 = 125 As we know, from the formula of the nth term in an AP, an = a +(n−1)d, Therefore, putting the given values, we get, a3 = a+(3−1)d 15 = a+2d ………………………….. (i) Sum of the nth term, Sn = n/2 [2a+(n-1)d] S10 = 10/2 [2a+(10-1)d] 125 = 5(2a+9d) 25 = 2a+9d ……………………….. (ii) On multiplying equation (i) by (ii), we will get; 30 = 2a+4d ………………………………. (iii) By subtracting equation (iii) from (ii), we get, −5 = 5d d = −1 From equation (i), 15 = a+2(−1) 15 = a−2 a = 17 = First term a10 = a+(10−1)d a10 = 17+(9)(−1) a10 = 17−9 = 8

(v) Given that, d = 5, S9 = 75 As, sum of n terms in AP is, Sn = n/2 [2a +(n -1)d] Therefore, the sum of first nine terms are; S9 = 9/2 [2a +(9-1)5] 25 = 3(a+20) 25 = 3a+60 3a = 25−60 a = -35/3 As we know, the nth term can be written as; an = a+(n−1)d a9 = a+(9−1)(5) = -35/3+8(5) = -35/3+40 = (35+120/3) = 85/3

(vi) Given that, a = 2, d = 8, Sn = 90 As, sum of n terms in an AP is, Sn = n/2 [2a +(n -1)d] 90 = n/2 [2a +(n -1)d] ⇒ 180 = n(4+8n -8) = n(8n-4) = 8n2-4n ⇒ 8n2-4n –180 = 0 ⇒ 2n2–n-45 = 0 ⇒ 2n2-10n+9n-45 = 0 ⇒ 2n(n -5)+9(n -5) = 0 ⇒ (n-5)(2n+9) = 0 So, n = 5 (as n only be a positive integer) ∴ a5 = 8+5×4 = 34

(vii) Given that, a = 8, an = 62, Sn = 210 As, sum of n terms in an AP is, Sn = n/2 (a + an) 210 = n/2 (8 +62) ⇒ 35n = 210 ⇒ n = 210/35 = 6 Now, 62 = 8+5d ⇒ 5d = 62-8 = 54 ⇒ d = 54/5 = 10.8

(viii) Given that, nth term, an = 4, common difference, d = 2, sum of n terms, Sn = −14. As we know, from the formula of the nth term in an AP, an = a+(n −1)d, Therefore, putting the given values, we get, 4 = a+(n −1)2 4 = a+2n−2 a+2n = 6 a = 6 − 2n …………………………………………. (i) As we know, the sum of n terms is; Sn = n/2 (a+an) -14 = n/2 (a+4) −28 = n (a+4) −28 = n (6 −2n +4) {From equation (i)} −28 = n (− 2n +10) −28 = − 2n2+10n 2n2 −10n − 28 = 0 n2 −5n −14 = 0 n2 −7n+2n −14 = 0 n (n−7)+2(n −7) = 0 (n −7)(n +2) = 0 Either n − 7 = 0 or n + 2 = 0 n = 7 or n = −2 However, n can neither be negative nor fractional. Therefore, n = 7 From equation (i), we get a = 6−2n a = 6−2(7) = 6−14 = −8

(ix) Given that, first term, a = 3, Number of terms, n = 8 And sum of n terms, S = 192 As we know, Sn = n/2 [2a+(n -1)d] 192 = 8/2 [2×3+(8 -1)d] 192 = 4[6 +7d] 48 = 6+7d 42 = 7d d = 6

(x) Given that, l = 28,S = 144 and there are total of 9 terms. Sum of n terms formula, Sn = n/2 (a + l) 144 = 9/2(a+28) (16)×(2) = a+28 32 = a+28 a = 4

4. How many terms of the AP. 9, 17, 25 … must be taken to give a sum of 636?

Solutions: Let there be n terms of the AP. 9, 17, 25 … For this A.P., First term, a = 9 Common difference, d = a2−a1 = 17−9 = 8 As, the sum of n terms, is; Sn = n/2 [2a+(n -1)d] 636 = n/2 [2×a+(8-1)×8] 636 = n/2 [18+(n-1)×8] 636 = n [9 +4n −4] 636 = n (4n +5) 4n2 +5n −636 = 0 4n2 +53n −48n −636 = 0 n (4n + 53)−12 (4n + 53) = 0 (4n +53)(n −12) = 0 Either 4n+53 = 0 or n−12 = 0 n = (-53/4) or n = 12 n cannot be negative or fraction, therefore, n = 12 only.

5. The first term of an AP is 5, the last term is 45 and the sum is 400. Find the number of terms and the common difference.

Solution: Given that, first term, a = 5 last term, l = 45 Sum of the AP, Sn = 400 As we know, the sum of AP formula is; Sn = n/2 (a+l) 400 = n/2(5+45) 400 = n/2(50) Number of terms, n =16 As we know, the last term of AP series can be written as; l = a+(n −1)d 45 = 5 +(16 −1)d 40 = 15d Common difference, d = 40/15 = 8/3

6. The first and the last term of an AP are 17 and 350 respectively. If the common difference is 9, how many terms are there and what is their sum?

Solution: Given that, First term, a = 17 Last term, l = 350 Common difference, d = 9 Let there be n terms in the A.P., thus the formula for last term can be written as; l = a+(n −1)d 350 = 17+(n −1)9 333 = (n−1)9 (n−1) = 37 n = 38 Sn = n/2 (a+l) S38 = 38/2 (17+350) = 19×367 = 6973 Thus, this A.P. contains 38 terms and the sum of the terms of this A.P. is 6973.

7. Find the sum of first 22 terms of an AP in which d = 7 and 22nd term is 149.

Solution: Given,

Common difference, d = 7 22nd term, a22 = 149 Sum of first 22 term, S22 = ? By the formula of nth term, an = a+(n−1)d a22 = a+(22−1)d 149 = a+21×7 149 = a+147 a = 2 = First term Sum of n terms, Sn = n/2(a+an) S22 = 22/2 (2+149) = 11×151 = 1661

8. Find the sum of first 51 terms of an AP whose second and third terms are 14 and 18 respectively.

Solution: Given that, Second term, a2 = 14 Third term, a3 = 18 Common difference, d = a3−a2 = 18−14 = 4 a2 = a+d 14 = a+4 a = 10 = First term Sum of n terms; Sn = n/2 [2a + (n – 1)d] S51 = 51/2 [2×10 (51-1) 4] = 51/2 [20+(50)×4] = 51 × 220/2 = 51 × 110 = 5610

9. If the sum of first 7 terms of an AP is 49 and that of 17 terms is 289, find the sum of first n terms.

Solution: Given that, S7 = 49 S17 = 289 We know, Sum of n terms; Sn = n/2 [2a + (n – 1)d] Therefore, S7= 7/2 [2a +(n -1)d] S7 = 7/2 [2a + (7 -1)d] 49 = 7/2 [2a +6d] 7 = (a+3d) a + 3d = 7 …………………………………. (i) In the same way, S17 = 17/2 [2a+(17-1)d] 289 = 17/2 (2a +16d) 17 = (a+8d) a +8d = 17 ………………………………. (ii) Subtracting equation (i) from equation (ii), 5d = 10 d = 2 From equation (i), we can write it as; a+3(2) = 7 a+ 6 = 7 a = 1 Hence, Sn = n/2[2a+(n-1)d] = n/2[2(1)+(n – 1)×2] = n/2(2+2n-2) = n/2(2n) = n2

10. Show that a1, a2 … , an , … form an AP where an is defined as below (i) an = 3+4n (ii) an = 9−5n Also find the sum of the first 15 terms in each case.

Solutions: (i) an = 3+4n a1 = 3+4(1) = 7 a2 = 3+4(2) = 3+8 = 11 a3 = 3+4(3) = 3+12 = 15 a4 = 3+4(4) = 3+16 = 19 We can see here, the common difference between the terms are; a2 − a1 = 11−7 = 4 a3 − a2 = 15−11 = 4 a4 − a3 = 19−15 = 4 Hence, ak + 1 − ak is the same value every time. Therefore, this is an AP with common difference as 4 and first term as 7. Now, we know, the sum of nth term is; Sn = n/2[2a+(n -1)d] S15 = 15/2[2(7)+(15-1)×4] = 15/2[(14)+56] = 15/2(70) = 15×35 = 525

(ii) an = 9−5n a1 = 9−5×1 = 9−5 = 4 a2 = 9−5×2 = 9−10 = −1 a3 = 9−5×3 = 9−15 = −6 a4 = 9−5×4 = 9−20 = −11 We can see here, the common difference between the terms are; a2 − a1 = −1−4 = −5 a3 − a2 = −6−(−1) = −5 a4 − a3 = −11−(−6) = −5 Hence, ak + 1 − ak is same every time. Therefore, this is an A.P. with common difference as −5 and first term as 4. Now, we know, the sum of nth term is; Sn = n/2 [2a +(n-1)d] S15 = 15/2[2(4) +(15 -1)(-5)] = 15/2[8 +14(-5)] = 15/2(8-70) = 15/2(-62) = 15(-31) = -465

11. If the sum of the first n terms of an AP is 4n − n2, what is the first term (that is S1)? What is the sum of first two terms? What is the second term? Similarly find the 3rd, the10th and the nth terms.

Solution: Given that, Sn = 4n−n2 First term, a = S1 = 4(1) − (1)2 = 4−1 = 3 Sum of first two terms = S2= 4(2)−(2)2 = 8−4 = 4 Second term, a2 = S2 − S1 = 4−3 = 1 Common difference, d = a2−a = 1−3 = −2 Nth term, an = a+(n−1)d = 3+(n −1)(−2) = 3−2n +2 = 5−2n Therefore, a3 = 5−2(3) = 5-6 = −1 a10 = 5−2(10) = 5−20 = −15 Hence, the sum of first two terms is 4. The second term is 1. The 3rd, the 10th, and the nth terms are −1, −15, and 5 − 2n respectively.

12. Find the sum of first 40 positive integers divisible by 6.

Solution: The positive integers that are divisible by 6 are 6, 12, 18, 24 …. We can see here, that this series forms an A.P. whose first term is 6 and common difference is 6. a = 6 d = 6 S40 = ? By the formula of sum of n terms, we know, Sn = n/2 [2a +(n – 1)d] Therefore, putting n = 40, we get, S40 = 40/2 [2(6)+(40-1)6] = 20[12+(39)(6)] = 20(12+234) = 20×246 = 4920

13. Find the sum of first 15 multiples of 8.

Solution: The multiples of 8 are 8, 16, 24, 32… The series is in the form of AP, having first term as 8 and common difference as 8. Therefore, a = 8 d = 8 S15 = ? By the formula of sum of nth term, we know, Sn = n/2 [2a+(n-1)d] S15 = 15/2 [2(8) + (15-1)8] = 15/2[16 +(14)(8)] = 15/2[16 +112] = 15(128)/2 = 15 × 64 = 960

14. Find the sum of the odd numbers between 0 and 50.

Solution: The odd numbers between 0 and 50 are 1, 3, 5, 7, 9 … 49. Therefore, we can see that these odd numbers are in the form of A.P. Hence, First term, a = 1 Common difference, d = 2 Last term, l = 49 By the formula of last term, we know, l = a+(n−1) d 49 = 1+(n−1)2 48 = 2(n − 1) n − 1 = 24 n = 25 = Number of terms By the formula of sum of nth term, we know, Sn = n/2(a +l) S25 = 25/2 (1+49) = 25(50)/2 =(25)(25) = 625

15. A contract on construction job specifies a penalty for delay of completion beyond a certain date as follows: Rs. 200 for the first day, Rs. 250 for the second day, Rs. 300 for the third day, etc., the penalty for each succeeding day being Rs. 50 more than for the preceding day. How much money the contractor has to pay as penalty, if he has delayed the work by 30 days.

Solution: We can see, that the given penalties are in the form of A.P. having first term as 200 and common difference as 50. Therefore, a = 200 and d = 50 Penalty that has to be paid if contractor has delayed the work by 30 days = S30 By the formula of sum of nth term, we know, Sn = n/2[2a+(n -1)d] Therefore, S30= 30/2[2(200)+(30 – 1)50] = 15[400+1450] = 15(1850) = 27750 Therefore, the contractor has to pay Rs 27750 as penalty.

16. A sum of Rs 700 is to be used to give seven cash prizes to students of a school for their overall academic performance. If each prize is Rs 20 less than its preceding prize, find the value of each of the prizes.

Solution: Let the cost of 1st prize be Rs. P. Cost of 2nd prize = Rs. P − 20 And cost of 3rd prize = Rs. P − 40 We can see that the cost of these prizes are in the form of A.P., having common difference as −20 and first term as P. Thus, a = P and d = −20 Given that, S7 = 700 By the formula of sum of nth term, we know, Sn = n/2 [2a + (n – 1)d] 7/2 [2a + (7 – 1)d] = 700

a + 3(−20) = 100 a −60 = 100 a = 160 Therefore, the value of each of the prizes was Rs 160, Rs 140, Rs 120, Rs 100, Rs 80, Rs 60, and Rs 40.

17. In a school, students thought of planting trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be the same as the class, in which they are studying, e.g., a section of class I will plant 1 tree, a section of class II will plant 2 trees and so on till class XII. There are three sections of each class. How many trees will be planted by the students?

Solution: It can be observed that the number of trees planted by the students is in an AP. 1, 2, 3, 4, 5………………..12 First term, a = 1 Common difference, d = 2−1 = 1 Sn = n/2 [2a +(n-1)d] S12 = 12/2 [2(1)+(12-1)(1)] = 6(2+11) = 6(13) = 78 Therefore, number of trees planted by 1 section of the classes = 78 Number of trees planted by 3 sections of the classes = 3×78 = 234 Therefore, 234 trees will be planted by the students.

18. A spiral is made up of successive semicircles, with centres alternately at A and B, starting with centre at A of radii 0.5, 1.0 cm, 1.5 cm, 2.0 cm, ……… as shown in figure. What is the total length of such a spiral made up of thirteen consecutive semicircles? (Take π = 22/7)

Solution: We know, Perimeter of a semi-circle = πr Therefore, P1 = π(0.5) = π/2 cm P2 = π(1) = π cm P3 = π(1.5) = 3π/2 cm Where, P1, P2, P3 are the lengths of the semi-circles. Hence we got a series here, as, π/2, π, 3π/2, 2π, …. P1 = π/2 cm P2 = π cm Common difference, d = P2 – P1 = π – π/2 = π/2 First term = P1= a = π/2 cm By the sum of n term formula, we know, Sn = n/2 [2a + (n – 1)d] Therefor, Sum of the length of 13 consecutive circles is; S13 = 13/2 [2(π/2) + (13 – 1)π/2] =  13/2 [π + 6π] =13/2 (7π) = 13/2 × 7 × 22/7 = 143 cm

19. 200 logs are stacked in the following manner: 20 logs in the bottom row, 19 in the next row, 18 in the row next to it and so on. In how many rows are the 200 logs placed and how many logs are in the top row?

Solution: We can see that the numbers of logs in rows are in the form of an A.P.20, 19, 18… For the given A.P., First term, a = 20 and common difference, d = a2−a1 = 19−20 = −1 Let a total of 200 logs be placed in n rows. Thus, Sn = 200 By the sum of nth term formula, Sn = n/2 [2a +(n -1)d] S12 = 12/2 [2(20)+(n -1)(-1)] 400 = n (40−n+1) 400 = n (41-n) 400 = 41n−n2 n2−41n + 400 = 0 n2−16n−25n+400 = 0 n(n −16)−25(n −16) = 0 (n −16)(n −25) = 0 Either (n −16) = 0 or n−25 = 0 n = 16 or n = 25 By the nth term formula, an = a+(n−1)d a16 = 20+(16−1)(−1) a16 = 20−15 a16 = 5 Similarly, the 25th term could be written as; a25 = 20+(25−1)(−1) a25 = 20−24 = −4 It can be seen, the number of logs in 16th row is 5 as the numbers cannot be negative. Therefore, 200 logs can be placed in 16 rows and the number of logs in the 16th row is 5.

20. In a potato race, a bucket is placed at the starting point, which is 5 m from the first potato and other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line.

A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are in the bucket. What is the total distance the competitor has to run? [Hint: to pick up the first potato and the second potato, the total distance (in metres) run by a competitor is 2×5+2×(5+3)]

Solution: The distances of potatoes from the bucket are 5, 8, 11, 14…, which is in the form of AP. Given, the distance run by the competitor for collecting these potatoes are two times of the distance at which the potatoes have been kept. Therefore, distances to be run w.r.t distances of potatoes, could be written as; 10, 16, 22, 28, 34,………. Hence, the first term, a = 10 and d = 16−10 = 6 S10 =? By the formula of sum of n terms, we know, S10 = 10/2 [2(10)+(10 -1)(6)] = 5[20+54] = 5(74) = 370 Therefore, the competitor will run a total distance of 370 m.

Exercise 5.4

1. Which term of the AP: 121, 117, 113, . . ., is its first negative term? [Hint: Find n for an < 0]

Solution: Given the AP series is 121, 117, 113, . . ., Thus, first term, a = 121 Common difference, d = 117-121= -4 By the nth term formula, an = a+(n −1)d Therefore, an = 121+(n−1)(-4) = 121-4n+4 =125-4n To find the first negative term of the series, an < 0 Therefore, 125-4n < 0 125 < 4n n>125/4 n>31.25 Therefore, the first negative term of the series is 32nd term.

2. The sum of the third and the seventh terms of an AP is 6 and their product is 8. Find the sum of first sixteen terms of the AP.

Solution: From the given statements, we can write, a3 + a7 = 6 …………………………….(i) And a3 ×a7 = 8 ……………………………..(ii) By the nth term formula, an = a+(n−1)d Third term, a3 = a+(3 -1)d a3 = a + 2d………………………………(iii) And Seventh term, a7= a+(7-1)d a7 = a + 6d ………………………………..(iv) From equation (iii) and (iv), putting in equation(i), we get, a+2d +a+6d = 6 2a+8d = 6 a+4d=3 or a = 3–4d …………………………………(v) Again putting the eq.(iii) and (iv), in eq. (ii), we get, (a+2d)×(a+6d) = 8 Putting the value of a from equation (v), we get, (3–4d +2d)×(3–4d+6d) = 8 (3 –2d)×(3+2d) = 8 32 – 2d2 = 8 9 – 4d2 = 8 4d2 = 1 d = 1/2 or -1/2 Now, by putting both the values of d, we get, a = 3 – 4d = 3 – 4(1/2) = 3 – 2 = 1, when d = 1/2 a = 3 – 4d = 3 – 4(-1/2) = 3+2 = 5, when d = -1/2 We know, the sum of nth term of AP is; Sn = n/2 [2a +(n – 1)d] So, when a = 1 and d=1/2 Then, the sum of first 16 terms are; S16 = 16/2 [2 +(16-1)1/2] = 8(2+15/2) = 76 And when a = 5 and d= -1/2 Then, the sum of first 16 terms are; S16 = 16/2 [2(5)+(16-1)(-1/2)] = 8(5/2)=20

3. A ladder has rungs 25 cm apart. (see Fig. 5.7). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and the bottom rungs are

apart, what is the length of the wood required for the rungs? [Hint: Number of rungs = -250/25 ].

Solution: Given, Distance between the rungs of the ladder is 25cm. Distance between the top rung and bottom rung of the ladder is =

= 5/2 ×100cm = 250cm Therefore, total number of rungs = 250/25 + 1 = 11 As we can see from the figure, the ladder has rungs in decreasing order from top to bottom. Thus, we can conclude now, that the rungs are decreasing in an order of AP. And the length of the wood required for the rungs will be equal to the sum of the terms of AP series formed. So, First term, a = 45 Last term, l = 25 Number of terms, n = 11 Now, as we know, sum of nth terms is equal to, Sn= n/2(a+ l) Sn= 11/2(45+25) = 11/2(70) = 385 cm Hence, the length of the wood required for the rungs is 385cm.

4. The houses of a row are numbered consecutively from 1 to 49. Show that there is a value of x such that the sum of the numbers of the houses preceding the house numbered x is equal to the sum of the numbers of the houses following it. Find this value of x. [Hint :Sx – 1 = S49 – Sx ]

Solution: Given, Row houses are numbers from 1,2,3,4,5…….49. Thus we can see the houses numbered in a row are in the form of AP. So, First term, a = 1 Common difference, d=1 Let us say the number of xth houses can be represented as; Sum of nth term of AP = n/2[2a+(n-1)d] Sum of number of houses beyond x house = Sx-1 = (x-1)/2[2(1)+(x-1-1)1] = (x-1)/2 [2+x-2] = x(x-1)/2 ………………………………………(i) By the given condition, we can write, S49 – Sx = {49/2[2(1)+(49-1)1]}–{x/2[2(1)+(x-1)1]} = 25(49) – x(x + 1)/2 ………………………………….(ii) As per the given condition, eq.(i) and eq(ii) are equal to each other; Therefore, x(x-1)/2 = 25(49) – x(x+1)/2 x = ±35 As we know, the number of houses cannot be a negative number. Hence, the value of x is 35.

5. A small terrace at a football ground comprises of 15 steps each of which is 50 m long and built of solid concrete. Each step has a rise of 1 4 m and a tread of 1 2 m. (see Fig. 5.8). Calculate the total volume of concrete required to build the terrace. [Hint : Volume of concrete required to build the first step = ¼ ×1/2 ×50 m3.]

Solution: As we can see from the given figure, the first step is ½ m wide, 2nd step is 1m wide and 3rd step is 3/2m wide. Thus we can understand that the width of step by ½ m each time when height is ¼ m. And also, given length of the steps is 50m all the time. So, the width of steps forms a series AP in such a way that; ½ , 1, 3/2, 2, …….. Volume of steps = Volume of Cuboid = Length × Breadth Height Now, Volume of concrete required to build the first step = ¼ ×1/2 ×50 = 25/4 Volume of concrete required to build the second step =¼ ×1×50 = 25/2 Volume of concrete required to build the second step = ¼ ×3/2 ×50 = 75/4 Now, we can see the volumes of concrete required to build the steps, are in AP series; 25/4 , 25/2 , 75/4 ….. Thus, applying the AP series concept, First term, a = 25/4 Common difference, d = 25/2 – 25/4 = 25/4 As we know, the sum of n terms is; Sn = n/2[2a+(n-1)d] = 15/2(2×(25/4 )+(15/2 -1)25/4) Upon solving, we get, Sn = 15/2 (100) Sn=750 Hence, the total volume of concrete required to build the terrace is 750 m3.