Question 1.
The unit of correlation coefficient between height in feet and weight in kgs is
(a) kg/feet
(b) percentage
(c) non-existent
Answer:
(c) Correlation coefficient (r) has no unit. It is a pure number. It meansss units of measurement are not part of r.
Question 2.
The range of simple correlation coefficient is
(a) 0 to infinity
(b) minus one to plus one
(c) minus infinity to infinity
Answer:
(b) The value of the correlation coefficient lies between minus one and plus one, -1 ≤ r ≤ 1. If the value of r is outside this range it indicates error in calculation.
Question 3.
If rXYis positive the relation between X and Y is of the type
(a) when Y increases X increases
(b) when Y decreases X increases
(c) when Y increases X does not change
Answer:
(a) If r is positive the two variables move in the same direction. e.g., when the price of coffee rises, the demand for tea also rises as coffee is a substitute of tea. Therefore, the r between price of coffee and demand for tea will be positive.
Question 4.
If rXY= 0, the variable X and Y are
(a) linearly related
(b) not linearly related
(c) independent
Answer:
(b) If rXY= 0, it means the two variables are uncorrelated and there is no linear relation between them. However, other types of relation may be there and they may not be independent.
Question 5.
Of the following three measures which can measure any type of relationship?
(a) Karl Pearson’s coefficient of correlation
(b) Spearman’s rank correlation
(c) Scatter diagram
Answer:
(c) The scatter diagram gives a visual presentation of the relationship and is not confined to linear relations. Karl Pearson’s coefficient of correlation and Spearman’s rank correlation are strictly the measures of linear relationship.
Question 6.
If precisely measured data are available the simple correlation coefficient is
(a) more accurate than rank correlation coefficient
(b) less accurate than rank correlation coefficient
(c) as accurate as the rank correlation coefficient
Answer:
(a) Rank correlation should be used only when the variables cannot be measured precisely, generally it is not as accurate as the simple correlation coefficient as all the information concerning the data is not utilised in this.
Question 7.
Why is r preferred to covariance as a measure of association?
Answer:
Both, correlation coefficient and covariance measure the degree of linear relationship between two variables, but correlation coefficient is generally preferred to covariance due to the following reasons
The correlation coefficient (r) has no unit.
The correlation coefficient is independent of origin as well as scale.
Question 8.
Can r lie outside the -1 and 1 range depending on the type of data?
Answer:
No the value of the correlation coefficient lies between minus one and plus one, -1 ≤ r ≤ 1. If the value of r is outside this range in any type of data, it indicates error in calculation.
Question 9.
Does correlation imply causation?
Answer:
No, correlation measures do not imply causation. Correlation measures co-variation and not causation.
Correlation does not imply cause and effect relation. The knowledge of correlation only gives us an idea of the direction and intensity of change in a variable when the correlated variable changes. The presence of correlation between two variables X and Y simply means that when the value of one variable is found to change in one direction, the value of the other variable is found to change either in the same direction (i.epositive change) or in the opposite direction (i.e., negative change), in a definite way.
Question 10.
When is rank correlation more precise than simple correlation coefficient?
Answer:
Rank correlation is more precise than simple correlation coefficient in the following situations
When the Measurements of the Variables are Suspect e.g., in a remote village where measuring rods or weighing scales are not available, height and weight of people cannot be measured precisely but the people can be easily ranked in terms of height and weight.
When Data is Qualitative It is difficult to quantify qualities such as fairness, honesty etc. Ranking may be a better alternative to quantification of qualities.
When Data has Extreme Values Sometimes the correlation coefficient between two variables with extreme values may be quite different from the coefficient without the extreme values. Under these circumstances rank correlation provides a better alternative to simple correlation.
Question 11.
Does zero correlation mean independence?
Answer:
No, zero correlation does not mean independence. If there is zero correlation (rXY= 0), it means the two variables are uncorrelated and there is no linear relation between them. However, other types of relation may be there and they may not be independent.
Question 12.
Can simple correlation coefficient measure any type of relationship?
Answer:
No, simple correlation coefficient can measure only linear relationship.
Question 13.
List some variables where accurate measurement is difficult.
Answer:
Accurate measurement is difficult in case of
Qualitative variables such as beauty, intelligence, honesty, etc.
It is also difficult to measure subjective variables such as poverty, development, etc which are interpreted differently by different people.
Question 14.
Interpret the values of r as 1, -1 and 0.
Answer:
If r = 0 the two variables are uncorrelated. There is no linear relation between them. However, other types of relation may be there and hence the variables may not be independent.
If r= 1 the correlation is perfectly positive. The relation between them is exact in the sense that if one increases, the other also increases in the same proportion and if one decreases, the other also decreases in the same proportion.
If r = -1 the correlation is perfectly negative. The relation between them is exact in the sense that if one increases, the other decreases in the same proportion and if one decreases, the other increases in the same proportion.
Question 15.
Why does rank correlation coefficient differ from Pearsonian correlation coefficient?
Answer:
Rank correlation coefficient differs from Pearsonian correlation coefficient in the following ways
Rank correlation coefficient is generally lower or equal to Karl Pearson’s coefficient.
Rank correlation coefficient is preferred to measure the correlation between qualitative variables as these variables cannot be measured precisely.
The rank correlation coefficient uses ranks instead of the full set of observations that leads to some loss of information.
If extreme values are present in the data, then the rank correlation coefficient is more precise and reliable.
Question 16.
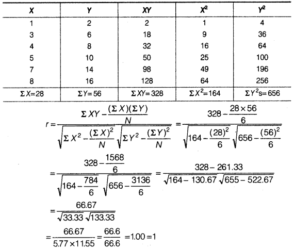
Calculate the correlation coefficient between the heights of fathers in inches (X) and their sons (Y).
![]()
Answer:
Note Answer: printed in NCERT is incorrect.
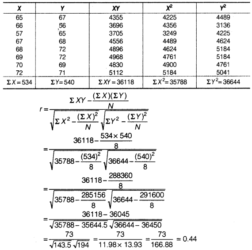
Question 17.
Calculate the correlation coefficient between X and Y and comment on their relationship.
![]()
Answer:
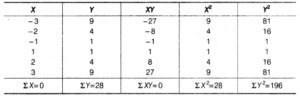
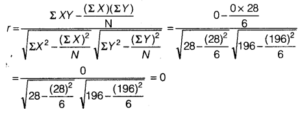
As the value of r is zero, so there is no linear correlation between X and Y.
Question 18.
Calculate the correlation coefficient between X and Y and comment on their relationship.
![]()
Solution