Class 10 Maths Exam Today’s Term 2 Question Paper & Answer Key Soon

Unlike the Class 10 English exam, the Maths paper was lengthy, as per some students, who came out from the centers after writing it.

Section A that had 2 marks questions was easy to solve. It took much time because it required step-by-step answers. However, students, who wrote the Standards Maths exam, seemed unhappy as they didn’t expect the level of the paper in term 2, considering it was their first subjective exam in the last two years.

The examination was moderate to hard as many think that they will get good marks. It’s important to mention that CBSE held the first-term examinations in November-December 2021.

Maths (Class 10) Term 2 Question Paper 2022

General Instructions:

1. This question paper contains 14 questions. All questions are compulsory.
2. This Question Paper is divided into 3 Sections – Section A, B and C.
3. Section A comprises of 6 questions (Q. Nos. 1 to 6) of 2 marks each. Internal choice has been provided in two questions.
4. Section B comprises of 4 questions (Q. Nos. 7 to 10) of 3 marks each. Internal choice has been provided in one question.
5. Section-C comprises of 4 questions (Q. Nos. 11 to 14) of 4 marks each. An
   internal choice has been provided in one question. It also contains two case study-based questions.
6. Use of a calculator is not permitted.

SECTION -A (Question Numbers 1 to 6 carry 2 marks each)

Question 1. A solid piece of metal in the form of a cuboid of dimensions 11 cm x 7 cm x 7 cm is melted to form ‘n’ number of solid spheres of radii 7/2cm each. Find the value of n.

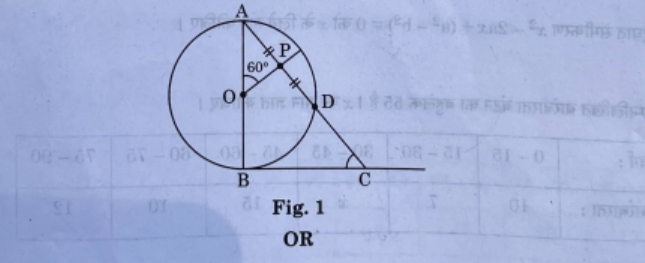
Question 2. (a) In Fig. 1, AB is diameter of a circle centered at O. BC is tangent to the circle at B. If OP bisects the chord AD and ∠AOP = 60°, then find
m∠C.

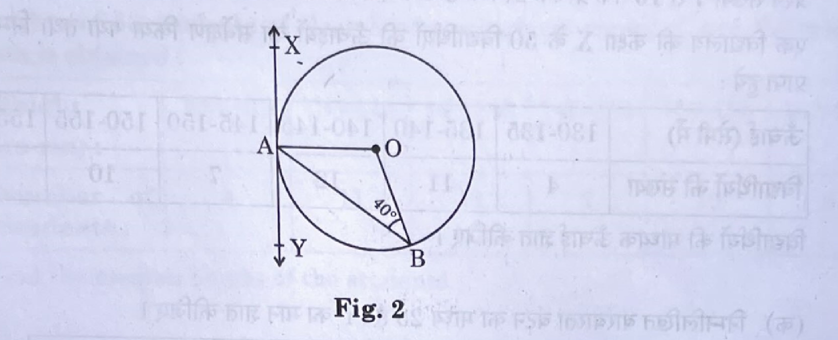
(b) In Fig. 2, XAY is a tangent to the circle centered at O. If ∠ABO = 40°, then find m∠BAY and m∠AOB.

Question 3. (a) Which term of the A.P. -11/2,-3,-1/2,… is 49/2?

(b) Find a and b so that the numbers: a, 7, b, 23 are in A.P.

Question 4. Find the sum of the first 20 terms of an A.P. whose n^th term is given as a_n = 5 – 2n.

Question 5. Solve the quadratic equation : x² – 2ax + (a² – b²) = 0 for x.

Question 6. If the mode of the following frequency distribution is 55, then find the value of x.

Class	0-15	15-30	30-45	45-60	60-75	75-90
Frequency	10	7	2	15	10	12

 

Question Numbers from 7 to 10 carry 3 marks each.

Question 7. Heights of 50 students of class X of a school are recorded and following data is obtained:

Height (in cm)	130-135	135-140	140-145	145-150	150-155	155-160
Number of Students	4	11	12	7	10	6

Find the median height of the students.

Question 8. (a) The mean of the following frequency distribution is 25. Find the
value of f.

Class	0-10	20-Oct	20-30	30-40	40-50
Frequency	5	18	15	f	6

 

OR

(b) Find the mean of the following data using assumed mean method:

Class	0-5	5-10	10-15	15-20	20-25
Frequency	8	7	10	13	12

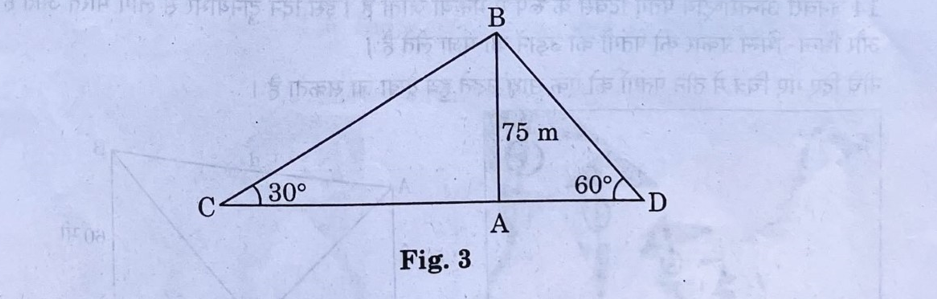
Question 9. Two men on either side of a cliff 75 m high observe the angles of elevation of the top of the cliff to be 30° and 60°. Find the distance between the two men.

Question 10. Construct a pair of tangents to a circle of radius 3 cm which are inclined to each other at an angle of 60°.

SECTION – C | Question Numbers from 11 to 14 carry 4 marks each.

Question 11. (a) The sum of two numbers is 34. If 3 is subtracted from one number and 2 is added to another, the product of these two numbers becomes 260. Find the numbers.

OR

(b) The hypotenuse (in cm) of a right angled triangle is 6 cm more than twice the length of the shortest side. If the length of third side is 6 cm less than thrice the length of shortest side, then find the dimensions of the triangle.

Question 12. In Fig. 4, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q meet at a point T. Find the length of TP.

Question 13. Case Study – 1: Kite Festival

Kite festival is celebrated in many countries at different times of the year. In India, every year 14th January is celebrated as International Kite Day. On this day many people visit India and participate in the festival by flying various kinds of kites.

The picture given below, shows three kites flying together.

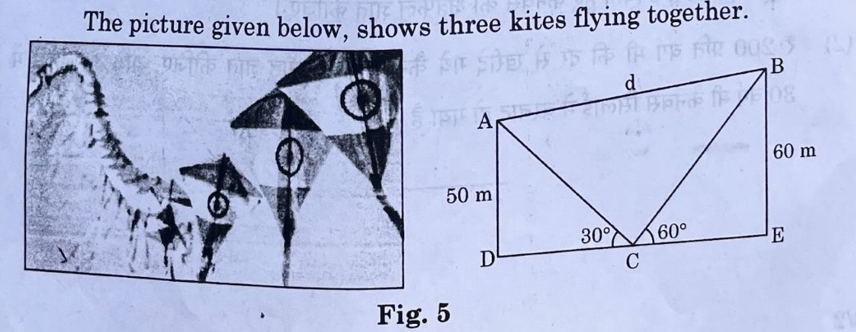
In Fig. 5, the angles of elevation of two kites (Points A and B) from the hands of a man (Point C) are found to be 30° and 60° respectively. Taking AD = 50 m and BE = 60 m, find

(1) the lengths of strings used (take them straight) for kites A and B as shown in the figure.

(2) the distance ‘d’ between these two kites

Question 14. Case Study – 2

A ‘circus’ is a company of performers who put on shows of acrobats, clowns etc. to entertain people started around 250 years back, in open fields, now generally performed in tents.

One such ‘Circus Tent’ is shown below.

The tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of cylindrical part are 9 m and 30 m respectively and height of conical part is 8 m with same diameter as that of the cylindrical part, then find

(1) the area of the canvas used in making the tent;

(2) the cost of the canvas bought for the tent at the rate ₹200 per sq m, if 30 sq m canvas was wasted during stitching.