Maths Class 10th Sample Question Paper to revise for Term 1 board exam.
Class – X | Session -2021-22 | TERM 1 | Subject- Mathematics (Standard) 041 | Time Allowed: 90 minutes | Maximum Marks: 40
It is often seen that most of the students fail to complete the Maths paper on time due to this they are not able to perform well in the exam. But if students read and understand the question paper with the right technique and strategy, then one will start finding it the most interesting subject. Apart from this, it is such a subject in which the student can score full marks. It is also seen that students get nervous while writing Maths exam due to which they are not able to solve all the questions correctly and miss to finish the exam on time. Due to the paucity of time students have to skip some important questions and it is often seen that those questions could have been solved easily.
Important things to keep in mind during the exam:
- First of all, understand the exam pattern closely
- Make sure to prepare a strategy before giving the exam
- Use the 20 minutes you get before writing the exam wisely
- Never be afraid of difficult questions
- Solve each question according to its importance and weight
- Keep Speed and Accuracy Together
General Instructions for Maths exam:
- The question paper contains three parts A, B and C
- Section A consists of 20 questions of 1 mark each. Any 16 questions are to be attempted
- Section B consists of 20 questions of 1 mark each. Any 16 questions are to be attempted
- Section C consists of 10 questions based on two Case Studies. Attempt any 8 questions.
- There is no negative marking.
| SECTION A |
|
|||
| Section A consists of 20 questions of 1 mark each. Any 16 questions are to be attempted | ||||
| Q No | Answer | |||
| 1 |
The ratio of LCM and HCF of the least composite and the least prime numbers is(a) 1:2 (b) 2:1 (c) 1:1 (d) 1:3 |
B | ||
| 2 |
The value of k for which the lines 5x+7y=3 and 15x + 21y = k coincide is(a) 9 (b) 5 (c) 7 (d) 18 |
A | ||
| 3 |
A girl walks 200m towards the East and then 150m towards the North. The distance of the girl from the starting point is(a)350m (b) 250m (c) 300m (d) 225 |
B | ||
| 4 |
The lengths of the diagonals of a rhombus are 24cm and 32cm, then the length of the altitude of the rhombus is(a) 12cm (b) 12.8cm (c) 19 cm` (d) 19.2cm |
D | ||
| 5 | Two fair coins are tossed. What is the probability of getting at the most one head?
(a) ¾ (b) ¼ (c) ½ (d) 3/8 |
A | ||
| 6 |
∆ABC~∆PQR. If AM and PN are altitudes of ∆ABC and ∆PQR respectively and AB2 :PQ2 = 4 : 9, then AM:PN = (a) 16:81 (b) 4:9 (c) 3:2 (d) 2:3 |
D | ||
| 7 |
If 2sin2β – cos2β = 2, then β is(a) 0ᵒ (b) 90ᵒ (c) 45ᵒ (d) 30ᵒ |
B | ||
| 8 |
Prime factors of the denominator of a rational number with the decimal expansion 44.123 are(a) 2,3 (b) 2,3,5 (c) 2,5 (d) 3,5 |
C | ||
| 9 |
The lines x = a and y = b, are(a) intersecting (b) parallel (c) overlapping (d) (None of these) |
A | ||
| 10 |
The distance of point A(-5, 6) from the origin is(a) 11 units (b) 61 units (c) √11 units (d) √61 units |
D | ||
| 11 |
If a² = 23/25, then a is(a) rational (b) irrational (c) whole number (d) integer |
B | ||
| 12 |
If LCM(x, 18) =36 and HCF(x, 18) =2, then x is(a) 2 (b) 3 (c) 4 (d) 5 |
C | ||
| 13 |
In ∆ABC right angled at B, if tan A= √3, then cos A cos C- sin A sin C =(a) -1 (b) 0 (c) 1 (d) √3/2 |
B | ||
| 14 |
If the angles of ∆ABC are in ratio 1:1:2, respectively (the largest angle being angle C), then the value of “sec A/cosec B” – “Tan A / cot B” is(a) 0 (b) 1/2 (c) 1 (d) √3/2 |
A | ||
| 15 |
The number of revolutions made by a circular wheel of radius 0.7m in rolling a distance of 176m is(a) 22 (b) 24 (c) 75 (d) 40 |
D | ||
| 16 |
∆ABC is such that AB=3 cm, BC= 2cm, CA= 2.5 cm. If ∆ABC ~ ∆DEF and EF = 4cm, then perimeter of ∆DEF is(a) 7.5 cm (b) 15 cm (c) 22.5 cm (d) 30 cm |
B | ||
| 17 |
In the figure, if DE BC, AD = 3cm, BD = 4cm and BC= 14 cm, then DE equals(a) 7cm (b) 6cm (c) 4cm (d) 3cm |
B | ||
| 18 |
If 4 tan β = 3, then (4 sinβ – 3 cosβ)/(4 sinβ + 3 cosβ ) =(a) 0 (b) 1/3 (c) 2/3 (d) ¾ |
A | ||
| 19 |
One equation of a pair of dependent linear equations is –5x + 7y = 2. The second equation can bea) 10x+14y +4 = 0 b) –10x –14y+ 4 = 0 c) –10x+14y + 4 = 0 (d) 10x – 14y = –4 |
D | ||
| 20 |
A letter of English alphabets is chosen at random. What is the probability that it is a letter of the word ‘MATHEMATICS’?(a) 4/13 (b) 9/26 (c) 5/13 (d) 11/26 |
A | ||
| SECTION B | ||||
| Section B consists of 20 questions of 1 mark each. Any 16 questions are to be attempted | ||||
| QN | MARKS | |||
| 21 |
If sum of two numbers is 1215 and their HCF is 81, then the possible number of pairs of such numbers are(a) 2 (b) 3 (c) 4 (d) 5 |
C | ||
| 22 |
Given below is the graph representing two linear equations by lines AB and CD respectively. What is the area of the triangle formed by these two lines and the line x=0?(a) 3sq. units (b) 4sq. units (c) 6sq. units (d) 8sq. units |
C | ||
| 23 |
If tan α + cot α = 2, then tan20α + cot20α =(a) 0 (b) 2 (c) 20 (d) 220 |
B | ||
| 24 |
If 217x + 131y = 913, 131x + 217y = 827, then x + y is(a) 5 (b) 6 (c) 7 (d) 8 |
A | ||
| 25 |
The LCM of two prime numbers p and q (p > q) is 221. Find the value of 3p – q.(a) 4 (b) 28 (c) 38 (d) 48 |
C | ||
| 26 |
A card is drawn from a well-shuffled deck of cards. What is the probability that the card drawn is neither a king nor a queen?(a) 11/13 (b) 12/13 (c) 11/26 (d) 11/52 |
A | ||
| 27 |
Two fair dice are rolled simultaneously. The probability that 5 will come up at least once is(a) 5/36 (b) 11/36 (c) 12/36 (d) 23/36 |
B | ||
| 28 |
If 1+ sin2α = 3 sinα cosα, then values of cot α are(a) -1, 1 (b) 0,1 (c)1, 2 (d) -1,-1 |
C | ||
| 29 |
The vertices of a parallelogram in order are A(1,2), B(4, y), C(x, 6) and D(3,5). Then (x, y) is(a) (6, 3) (b) (3, 6) (c) (5, 6) (d) (1, 4) |
A | ||
| 30 |
In the given figure, ∠ACB=∠CDA, AC = 8cm, AD = 3cm, then BD is(a) 22/3 cm (b) 26/3 cm (c) 55/3 cm (d) 64/3 cm |
C | ||
| 31 |
The equation of the perpendicular bisector of line segment joining points A(4,5) and B(-2,3) is(a) 2x – y +7=0 (b) 3x +2 y – 7=0 (c) 3x – y – 7 =0 (d) 3x + y – 7=0 |
D | ||
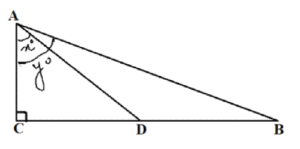
| 32 |
In the given figure, D is the mid-point of BC, then the value of cot y / cot x is
(a) 2 (b) 1/2 (c) 1/3 (d) 1/4 |
B | ||
| 33 |
The smallest number by which 1/13 should be multiplied so that its decimal expansion terminates after two decimal places is(a) 13/100 (b) 13/10 (c) 10/13 (d) 100/13 |
A | ||
| 34 |
Sides AB and BE of a right triangle, right angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of largest square FDGB that can be inscribed in the triangle ABE is(a) 32/3cm (b) 16/3cm (c)8/3cm (d) 4/3cm |
B | ||
| 35 |
Point P divides the line segment joining R(-1, 3) and S(9,8) in ratio k:1. If P lies on the line x – y +2=0, then value of k is(a) 2/3 (b) 1/2 (c) 1/3 (d) 1/4 |
A | ||
| 36 |
In the figure given below, ABCD is a square of side 14 cm with E, F, G and H as the midpoints of sides AB, BC, CD and DA respectively. The area of the shaded portion is(a) 44cm² (b) 49 cm² (c) 98 cm² (d) 49π/2 cm² |
C | ||
| 37 |
Given below is the picture of the Olympic rings made by taking five congruent circles of radius 1cm each, intersecting in such a way that the chord formed by joining the point of intersection of two circles is also of length 1cm. The total area of all the dotted regions assuming the thickness of the rings to be negligible is(a) 4(π/12-√3/4) cm² (b) (π/6 – √3/4) cm² (c) 4(π/6 – √3/4) cm² (d) 8(π/6 – √3/4) c |
D | ||
| 38 |
If 2 and ½ are the zeros of px2+5x+r, then(a) p = r = 2 (b) p = r = – 2 (c) p = 2, r= -2 (d) p = -2, r= 2 |
B | ||
| 39 |
The circumference of a circle is 100 cm. The side of a square inscribed in the circle is(a) 50√2 cm (b) 100/π cm (c) 50√2/π cm (d) 100√2/π cm |
C | ||
| 40 |
The number of solutions of 3x+y = 243 and 243x-y = 3 is(a) 0 (b) 1 (c) 2 (d) infinite |
B | ||
| SECTION C | ||||
| Case study based questions:
Section C consists of 10 questions of 1 mark each. Any 8 questions are to be attempted. |
||||
| Q41-Q45 are based on Case Study -1
Case Study -1 The figure given alongside shows the path of a diver, when she takes a jump from the diving board. Clearly it is a parabola. Annie was standing on a diving board, 48 feet above the water level. She took a dive into the pool. Her height (in feet) above the water level at any time‘t’ in seconds is given by the polynomial h(t) such that h(t) = -16t² + 8t + k. |
||||
| 41 |
What is the value of k?(a) 0 (b) – 48 (c) 48 (d) 48/-16 |
C | ||
| 42 |
At what time will she touch the water in the pool?(a) 30 seconds (b) 2 seconds (c) 1.5 seconds (d) 0.5 seconds |
B | ||
| 43 |
Rita’s height (in feet) above the water level is given by another polynomial p(t) with zeroes -1 and 2. Then p(t) is given by-(a) t² + t – 2. (b) t² + 2t – 1 (c) 24t² – 24t + 48. (d) -24t² + 24t + 48. |
D | ||
| 44 |
A polynomial q(t) with sum of zeroes as 1 and the product as -6 is modelling Anu’s height in feet above the water at any time t( in seconds). Then q(t) is given by(a) t² + t + 6 (b) t² + t -6 (c) -8t² + 8t + 48 (d) 8t² – 8t + 48 |
C | ||
| 45 |
The zeroes of the polynomial r(t) = -12t² + (k-3)t +48 are negative of each other. Then k is(a) 3 (b) 0 (c) -1.5 (d) -3 |
A | ||
| Q46-Q50 are based on Case Study -2 Case Study -2
A hockey field is a playing surface for the game of hockey. Historically, the game was played on natural turf (grass) but nowadays it is predominantly played on artificial turf. It is rectangular in shape – 100 yards by 60 yards. Goals consist of two upright posts placed equidistant from the centre of the backline, joined at the top by a horizontal crossbar. The inner edges of the posts must be 3.66 metres (4 yards) apart, and the lower edge of the crossbar must be 2.14 metres (7 feet) above the ground. Each team plays with 11 players on the field during the game including the goalie. Positions you might play include- • Forward: As shown by players A, B, C and D. • Midfielders: As shown by players E, F and G. • Fullbacks: As shown by players H, I and J. • Goalie: As shown by player K Using the picture of a hockey field below, answer the questions that follow: |
||||
| 46 |
The coordinates of the centroid of ΔEHJ are(a) (-2/3, 1) (b) (1,-2/3) (c) (2/3,1) (d) ( -2/3,-1) |
A | ||
| 47 |
If a player P needs to be at equal distances from A and G, such that A, P and G are in straight line, then position of P will be given by(a) (-3/2, 2) (b) (2,-3/2) (c) (2, 3/2) (d) ( -2,-3) |
C | ||
| 48 |
The point on x axis equidistant from I and E is(a) (1/2, 0) (b) (0,-1/2) (c) (-1/2,0) (d) ( 0,1/2) |
A | ||
| 49 |
What are the coordinates of the position of a player Q such that his distance from K is twice his distance from E and K, Q and E are collinear?(a) (1, 0) (b) (0,1) (c) (-2,1) (d) ( -1,0) |
B | ||
| 50 |
The point on y axis equidistant from B and C is(a) (-1, 0) (b) (0,-1) (c) (1,0) (d) ( 0,1) |
D | ||