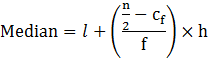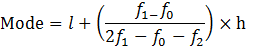Exercise 14.1
1. A survey was conducted by a group of students as a part of their environment awareness program, in which they collected the following data regarding the number of plants in 20 houses in a locality. Find the mean number of plants per house.
Number of Plants
0-2
2-4
4-6
6-8
8-10
10-12
12-14
Number of Houses
1
2
1
5
6
2
3
Which method did you use for finding the mean, and why?
Solution:
In order to find the mean value, we will use direct method because the numerical value of fiand xiare small.
Find the midpoint of the given interval using the formula.
Midpoint (xi) = (upper limit + lower limit)/2
No. of plants
(Class interval)
No. of houses
Frequency (fi)
Mid-point (xi)
fixi
0-2
1
1
1
2-4
2
3
6
4-6
1
5
5
6-8
5
7
35
8-10
6
9
54
10-12
2
11
22
12-14
3
13
39
Sum fi= 20
Sum fixi= 162
The formula to find the mean is:
Mean = x̄ = ∑fixi/∑fi
= 162/20
= 8.1
Therefore, the mean number of plants per house is 8.1
2. Consider the following distribution of daily wages of 50 workers of a factory.
Daily wages (in Rs.)
100-120
120-140
140-160
160-180
180-200
Number of workers
12
14
8
6
10
Find the mean daily wages of the workers of the factory by using an appropriate method.
Solution:
Find the midpoint of the given interval using the formula.
Midpoint (xi) = (upper limit + lower limit)/2
In this case, the value of mid-point (xi) is very large, so let us assume the mean value, A = 150 and class interval is h = 20.
So, ui= (xi– A)/h = ui = (xi– 150)/20
Substitute and find the values as follows:
Daily wages
(Class interval)
Number of workers
frequency (fi)
Mid-point (xi)
ui= (xi– 150)/20
fiui
100-120
12
110
-2
-24
120-140
14
130
-1
-14
140-160
8
150
0
0
160-180
6
170
1
6
180-200
10
190
2
20
Total
Sum fi= 50
Sum fiui= -12
So, the formula to find out the mean is:
Mean = x̄ = A + h∑fiui/∑fi=150 + (20 × -12/50) = 150 – 4.8 = 145.20
Thus, mean daily wage of the workers = Rs. 145.20
3. The following distribution shows the daily pocket allowance of children of a locality. The mean pocket allowance is Rs 18. Find the missing frequency f.
Daily Pocket Allowance(in c)
11-13
13-15
15-17
17-19
19-21
21-23
23-35
Number of children
7
6
9
13
f
5
4
Solution:
To find out the missing frequency, use the mean formula.
Here, the value of mid-point (xi) meanx̄= 18
Class interval
Number of children (fi)
Mid-point (xi)
fixi
11-13
7
12
84
13-15
6
14
84
15-17
9
16
144
17-19
13
18 = A
234
19-21
f
20
20f
21-23
5
22
110
23-25
4
24
96
Total
fi= 44+f
Sum fixi= 752+20f
The mean formula is
Mean = x̄ = ∑fixi/∑fi= (752+20f)/(44+f)
Now substitute the values and equate to find the missing frequency (f)
⇒ 18 = (752+20f)/(44+f)
⇒ 18(44+f) = (752+20f)
⇒ 792+18f = 752+20f
⇒ 792+18f = 752+20f
⇒ 792 – 752 = 20f – 18f
⇒ 40 = 2f
⇒ f = 20
So, the missing frequency, f = 20.
4. Thirty women were examined in a hospital by a doctor and the number of heart beats per minute were recorded and summarized as follows. Find the mean heart beats per minute for these women, choosing a suitable method.
Number of heart beats per minute
65-68
68-71
71-74
74-77
77-80
80-83
83-86
Number of women
2
4
3
8
7
4
2
Solution:
From the given data, let us assume the mean as A = 75.5
xi= (Upper limit + Lower limit)/2
Class size (h) = 3
Now, find the uiand fiuias follows:
Class Interval
Number of women (fi)
Mid-point (xi)
ui= (xi– 75.5)/h
fiui
65-68
2
66.5
-3
-6
68-71
4
69.5
-2
-8
71-74
3
72.5
-1
-3
74-77
8
75.5
0
0
77-80
7
78.5
1
7
80-83
4
81.5
3
8
83-86
2
84.5
3
6
Sum fi= 30
Sum fiui= 4
Mean = x̄ = A + h∑fiui/∑fi
= 75.5 + 3×(4/30)
= 75.5 + 4/10
= 75.5 + 0.4
= 75.9
Therefore, the mean heart beats per minute for these women is 75.9
5. In a retail market, fruit vendors were selling mangoes kept in packing boxes. These boxes contained varying number of mangoes. The following was the distribution of mangoes according to the number of boxes.
Number of mangoes
50-52
53-55
56-58
59-61
62-64
Number of boxes
15
110
135
115
25
Find the mean number of mangoes kept in a packing box. Which method of finding the mean did you choose?
Solution:
Since, the given data is not continuous so we add 0.5 to the upper limit and subtract 0.45 from the lower limit as the gap between two intervals are 1
Here, assumed mean (A) = 57
Class size (h) = 3
Here, the step deviation is used because the frequency values are big.
Class Interval
Number of boxes (fi)
Mid-point (xi)
di= xi– A
fidi
49.5-52.5
15
51
-6
90
52.5-55.5
110
54
-3
-330
55.5-58.5
135
57 = A
0
0
58.5-61.5
115
60
3
345
61.5-64.5
25
63
6
150
Sum fi= 400
Sum fidi= 75
The formula to find out the Mean is:
Mean = x̄ = A +h ∑fidi/∑fi
= 57 + 3(75/400)
= 57 + 0.1875
= 57.19
Therefore, the mean number of mangoes kept in a packing box is 57.19
6. The table below shows the daily expenditure on food of 25 households in a locality. Find the mean daily expenditure on food by a suitable method.
Daily expenditure(in c)
100-150
150-200
200-250
250-300
300-350
Number of households
4
5
12
2
2
Solution:
Find the midpoint of the given interval using the formula.
Midpoint (xi) = (upper limit + lower limit)/2
Let is assume the mean (A) = 225
Class size (h) = 50
Class Interval
Number of households (fi)
Mid-point (xi)
di= xi– A
ui= di/50
fiui
100-150
4
125
-100
-2
-8
150-200
5
175
-50
-1
-5
200-250
12
225
0
0
0
250-300
2
275
50
1
2
300-350
2
325
100
2
4
Sum fi= 25
Sum fiui= -7
Mean = x̄ = A +h∑fiui/∑fi
= 225+50(-7/25)
= 225-14
= 211
Therefore, the mean daily expenditure on food is 211
7. To find out the concentration of SO2in the air (in parts per million, i.e., ppm), the data was collected for 30 localities in a certain city and is presented below:
Concentration of SO2( in ppm)
Frequency
0.00 – 0.04
4
0.04 – 0.08
9
0.08 – 0.12
9
0.12 – 0.16
2
0.16 – 0.20
4
0.20 – 0.24
2
Find the mean concentration of SO2in the air.
Solution:
To find out the mean, first find the midpoint of the given frequencies as follows:
Concentration of SO2(in ppm)
Frequency (fi)
Mid-point (xi)
fixi
0.00-0.04
4
0.02
0.08
0.04-0.08
9
0.06
0.54
0.08-0.12
9
0.10
0.90
0.12-0.16
2
0.14
0.28
0.16-0.20
4
0.18
0.72
0.20-0.24
2
0.20
0.40
Total
Sum fi= 30
Sum (fixi) = 2.96
The formula to find out the mean is
Mean = x̄ = ∑fixi/∑fi
= 2.96/30
= 0.099 ppm
Therefore, the mean concentration of SO2in air is 0.099 ppm.
8. A class teacher has the following absentee record of 40 students of a class for the whole
term. Find the mean number of days a student was absent.
Number of days
0-6
6-10
10-14
14-20
20-28
28-38
38-40
Number of students
11
10
7
4
4
3
1
Solution:
Find the midpoint of the given interval using the formula.
Midpoint (xi) = (upper limit + lower limit)/2
Class interval
Frequency (fi)
Mid-point (xi)
fixi
0-6
11
3
33
6-10
10
8
80
10-14
7
12
84
14-20
4
17
68
20-28
4
24
96
28-38
3
33
99
38-40
1
39
39
Sumfi= 40
Sumfixi= 499
The mean formula is,
Mean = x̄ = ∑fixi/∑fi
= 499/40
= 12.48 days
Therefore, the mean number of days a student was absent = 12.48.
9. The following table gives the literacy rate (in percentage) of 35 cities. Find the mean
literacy rate.
Literacy rate (in %)
45-55
55-65
65-75
75-85
85-98
Number of cities
3
10
11
8
3
Solution:
Find the midpoint of the given interval using the formula.
Midpoint (xi) = (upper limit + lower limit)/2
In this case, the value of mid-point (xi) is very large, so let us assume the mean value, A = 70 and class interval is h = 10.
So, ui= (xi-A)/h = ui= (xi-70)/10
Substitute and find the values as follows:
Class Interval
Frequency (fi)
(xi)
di=xi– a
ui= di/h
fiui
45-55
3
50
-20
-2
-6
55-65
10
60
-10
-1
-10
65-75
11
70
0
0
0
75-85
8
80
10
1
8
85-95
3
90
20
2
6
Sumfi= 35
Sumfiui = -2
So, Mean = x̄ = A+(∑fiui/∑fi)×h
= 70+(-2/35)×10
= 69.42
Therefore, the mean literacy part = 69.42
Exercise 14.2
1. The following table shows the ages of the patients admitted in a hospital during a year:
Age (in years)
5-15
15-25
25-35
35-45
45-55
55-65
Number of patients
6
11
21
23
14
5
Find the mode and the mean of the data given above. Compare and interpret the two
measures of central tendency.
Solution:
To find out the modal class, let us the consider the class interval with high frequency
Here, the greatest frequency = 23, so the modal class = 35 – 45,
l = 35,
class width (h) = 10,
fm= 23,
f1= 21 and f2= 14
The formula to find the mode is
Mode= l+ [(fm-f1)/(2fm-f1-f2)]×h
Substitute the values in the formula, we get
Mode = 35+[(23-21)/(46-21-14)]×10
Mode = 35+(20/11) = 35+1.8
Mode = 36.8 year
So the mode of the given data = 36.8 year
Calculation of Mean:
First find the midpoint using the formula, xi= (upper limit +lower limit)/2
Class Interval
Frequency (fi)
Mid-point (xi)
fixi
5-15
6
10
60
15-25
11
20
220
25-35
21
30
630
35-45
23
40
920
45-55
14
50
700
55-65
5
60
300
Sumfi= 80
Sumfixi= 2830
The mean formula is
Mean = x̄ = ∑fixi/∑fi
= 2830/80
= 35.37 years
Therefore, the mean of the given data = 35.37 years
2. The following data gives the information on the observed lifetimes (in hours) of 225
electrical components:
Lifetime (in hours)
0-20
20-40
40-60
60-80
80-100
100-120
Frequency
10
35
52
61
38
29
Determine the modal lifetimes of the components.
Solution:
From the given data the modal class is 60–80.
l = 60,
The frequencies are:
fm= 61, f1= 52, f2= 38 and h = 20
The formula to find the mode is
Mode= l+ [(fm-f1)/(2fm-f1-f2)]×h
Substitute the values in the formula, we get
Mode =60+[(61-52)/(122-52-38)]×20
Mode = 60+((9 x 20)/32)
Mode = 60+(45/8) = 60+ 5.625
Therefore, modal lifetime of the components = 65.625 hours.
3. The following data gives the distribution of total monthly household expenditure of 200
families of a village. Find the modal monthly expenditure of the families. Also, find the
mean monthly expenditure:
Expenditure
Number of families
1000-1500
24
1500-2000
40
2000-2500
33
2500-3000
28
3000-3500
30
3500-4000
22
4000-4500
16
4500-5000
7
Solution:
Given data:
Modal class = 1500-2000,
l= 1500,
Frequencies:
fm= 40 f1= 24, f2= 33 and
h = 500
Mode formula:
Mode= l+ [(fm-f1)/(2fm-f1-f2)]×h
Substitute the values in the formula, we get
Mode =1500+[(40-24)/(80-24-33)]×500
Mode = 1500+((16×500)/23)
Mode = 1500+(8000/23) = 1500 + 347.83
Therefore, modal monthly expenditure of the families = Rupees 1847.83
Calculation for mean:
First find the midpoint using the formula, xi=(upper limit +lower limit)/2
Let us assume a mean, A be 2750
Class Interval
fi
xi
di = xi – a
ui = di/h
fiui
1000-1500
24
1250
-1500
-3
-72
1500-2000
40
1750
-1000
-2
-80
2000-2500
33
2250
-500
-1
-33
2500-3000
28
2750
0
0
0
3000-3500
30
3250
500
1
30
3500-4000
22
3750
1000
2
44
4000-4500
16
4250
1500
3
48
4500-5000
7
4750
2000
4
28
fi = 200
fiui = -35
The formula to calculate the mean,
Mean = x̄ = a +(∑fiui/∑fi)×h
Substitute the values in the given formula
= 2750+(-35/200)×500
= 2750-87.50
= 2662.50
So, the mean monthly expenditure of the families = Rupees 2662.50
4. The following distribution gives the state-wise teacher-student ratio in higher secondary schools of India. Find the mode and mean of this data. Interpret the two measures
No of Students per teacher
Number of states / U.T
15-20
3
20-25
8
25-30
9
30-35
10
35-40
3
40-45
0
45-50
0
50-55
2
Solution:
Given data:
Modal class = 30 – 35,
l= 30,
Class width (h) = 5,
fm= 10, f1= 9 and f2= 3
Mode Formula:
Mode= l+ [(fm-f1)/(2fm-f1-f2)]×h
Substitute the values in the given formula
Mode = 30+((10-9)/(20-9-3))×5
Mode = 30+(5/8) = 30+0.625
Mode = 30.625
Therefore, the mode of the given data = 30.625
Calculation of mean:
Find the midpoint using the formula, xi=(upper limit +lower limit)/2
Class Interval
Frequency (fi)
Mid-point (xi)
fixi
15-20
3
17.5
52.5
20-25
8
22.5
180.0
25-30
9
27.5
247.5
30-35
10
32.5
325.0
35-40
3
37.5
112.5
40-45
0
42.5
0
45-50
0
47.5
0
50-55
2
52.5
105.5
Sumfi= 35
Sumfixi= 1022.5
Mean = x̄ = ∑fixi/∑fi
= 1022.5/35
= 29.2
Therefore, mean = 29.2
5. The given distribution shows the number of runs scored by some top batsmenof the world in one- day international cricket matches.
Run Scored
Number of Batsman
3000-4000
4
4000-5000
18
5000-6000
9
6000-7000
7
7000-8000
6
8000-9000
3
9000-10000
1
10000-11000
1
Find the mode of the data.
Solution:
Given data:
Modal class = 4000 – 5000,
l = 4000,
class width (h) = 1000,
fm= 18, f1= 4 and f2= 9
Mode Formula:
Mode= l+ [(fm-f1)/(2fm-f1-f2)]×h
Substitute the values
Mode = 4000+((18-4)/(36-4-9))×1000
Mode = 4000+(14000/23) = 4000+608.695
Mode = 4608.695
Mode = 4608.7 (approximately)
Thus, the mode of the given data is 4608.7 runs
6. A student noted the number of cars passing through a spot on a road for 100 periods each of3 minutes and summarized it in the table given below. Find the mode of the data:
Number of cars
Frequency
0-10
7
10-20
14
20-30
13
30-40
12
40-50
20
50-60
11
60-70
15
70-80
8
Solution:
Given Data:
Modal class = 40 – 50, l = 40,
Class width (h) = 10, fm= 20, f1= 12 and f2= 11
Mode= l+ [(fm-f1)/(2fm-f1-f2)]×h
Substitute the values
Mode = 40+((20-12)/(40-12-11))×10
Mode = 40 + (80/17) = 40 + 4.7 = 44.7
Thus, the mode of the given data is 44.7 cars
Exercise 14.3
1. The following frequency distribution gives the monthly consumption of an electricity of 68 consumers in a locality. Find the median, mean and mode of the data and compare them.
Monthly consumption(in units)
No. of customers
65-85
4
85-105
5
105-125
13
125-145
20
145-165
14
165-185
8
185-205
4
Solution:
Find the cumulative frequency of the given data as follows:
Class Interval
Frequency
Cumulative frequency
65-85
4
4
85-105
5
9
105-125
13
22
125-145
20
42
145-165
14
56
165-185
8
64
185-205
4
68
N=68
From the table, it is observed that, n = 68 and hencen/2=34
Hence, the median class is 125-145 with cumulative frequency = 42
Where,l= 125, n = 68, Cf= 22, f = 20, h = 20
Median is calculated as follows:
=125+((34−22)/20) × 20
=125+12 = 137
Therefore, median = 137
To calculate the mode:
Modal class = 125-145,
f1=20, f0=13, f2=14& h = 20
Mode formula:
Mode= l+ [(f1-f0)/(2f1-f0-f2)]×h
Mode = 125 + ((20-13)/(40-13-14))×20
=125+(140/13)
=125+10.77
=135.77
Therefore, mode = 135.77
Calculate the Mean:
Class Interval
fi
xi
di=xi-a
ui=di/h
fiui
65-85
4
75
-60
-3
-12
85-105
5
95
-40
-2
-10
105-125
13
115
-20
-1
-13
125-145
20
135
0
0
0
145-165
14
155
20
1
14
165-185
8
175
40
2
16
185-205
4
195
60
3
12
Sumfi= 68
Sumfiui= 7
x̄ =a+h ∑fiui/∑fi=135+20(7/68)
Mean=137.05
In this case, mean, median and mode are more/less equal in this distribution.
2. If the median of a distribution given below is 28.5 then, find the value of x & y.
Class Interval
Frequency
0-10
5
10-20
x
20-30
20
30-40
15
40-50
y
50-60
5
Total
60
Solution:
Given data, n = 60
Median of the given data = 28.5
Where, n/2= 30
Median class is 20 – 30 with a cumulative frequency = 25+x
Lower limit of median class,l= 20,
Cf= 5+x,
f = 20 & h = 10
Substitute the values
28.5=20+((30−5−x)/20) × 10
8.5 = (25 – x)/2
17 = 25-x
Therefore, x =8
Now, from cumulative frequency, we can identify the value of x + y as follows:
Since,
60=5+20+15+5+x+y
Now, substitute the value of x, to find y
60 = 5+20+15+5+8+y
y = 60-53
y = 7
Therefore, the value of x = 8 and y = 7.
3. The Life insurance agent found the following data for the distribution of ages of 100 policy holders. Calculate the median age, if policies are given only to thepersons whose age is 18 years onwards but less than the 60 years.
Age (in years)
Number of policy holder
Below 20
2
Below 25
6
Below 30
24
Below 35
45
Below 40
78
Below 45
89
Below 50
92
Below 55
98
Below 60
100
Solution:
Class interval
Frequency
Cumulative frequency
15-20
2
2
20-25
4
6
25-30
18
24
30-35
21
45
35-40
33
78
40-45
11
89
45-50
3
92
50-55
6
98
55-60
2
100
Given data: n = 100 andn/2= 50
Median class = 35-45
Then,l= 35, cf= 45, f = 33 & h = 5
Median = 35+((50-45)/33) × 5
= 35 + (5/33)5
= 35.75
Therefore, the median age = 35.75 years.
4. The lengths of 40 leaves in a plant are measured correctly to the nearest millimeter, and the data obtained is represented as in the following table:
Length (in mm)
Number of leaves
118-126
3
127-135
5
136-144
9
145-153
12
154-162
5
163-171
4
172-180
2
Find the median length of leaves.
Solution:
Since the data are not continuous reduce 0.5 in the lower limit and add 0.5 in the upper limit.
Class Interval
Frequency
Cumulative frequency
117.5-126.5
3
3
126.5-135.5
5
8
135.5-144.5
9
17
144.5-153.5
12
29
153.5-162.5
5
34
162.5-171.5
4
38
171.5-180.5
2
40
So, the data obtained are:
n = 40 andn/2= 20
Median class = 144.5-153.5
then,l= 144.5,
cf = 17, f = 12 & h = 9
Median = 144.5+((20-17)/12)×9
= 144.5+(9/4)
= 146.75mm
Therefore, the median length of the leaves = 146.75 mm.
5. The following table gives the distribution of a life time of 400 neon lamps.
Lifetime (in hours)
Number of lamps
1500-2000
14
2000-2500
56
2500-3000
60
3000-3500
86
3500-4000
74
4000-4500
62
4500-5000
48
Find the median lifetime of a lamp.
Solution:
Class Interval
Frequency
Cumulative
1500-2000
14
14
2000-2500
56
70
2500-3000
60
130
3000-3500
86
216
3500-4000
74
290
4000-4500
62
352
4500-5000
48
400
Data:
n = 400 &n/2= 200
Median class = 3000 – 3500
Therefore,l= 3000, Cf= 130,
f = 86 & h = 500
Median = 3000 + ((200-130)/86) × 500
= 3000 + (35000/86)
= 3000 + 406.97
= 3406.97
Therefore, the median life time of the lamps = 3406.97 hours
6. In this 100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in English alphabets in the surnames was obtained as follows:
Number of letters
1-4
4-7
7-10
10-13
13-16
16-19
Number of surnames
6
30
40
16
4
4
Determine the number of median letters in the surnames. Find the number of mean letters in the surnames and also, find the size of modal in the surnames.
Solution:
To calculate median:
Class Interval
Frequency
Cumulative Frequency
1-4
6
6
4-7
30
36
7-10
40
76
10-13
16
92
13-16
4
96
16-19
4
100
Given:
n = 100 &n/2= 50
Median class = 7-10
Therefore,l= 7, Cf= 36, f = 40 & h = 3
Median = 7+((50-36)/40) × 3
Median = 7+42/40
Median=8.05
Calculate the Mode:
Modal class = 7-10,
Where,l= 7, f1= 40, f0= 30, f2= 16 & h = 3
Mode = 7+((40-30)/(2×40-30-16)) × 3
= 7+(30/34)
= 7.88
Therefore mode = 7.88
Calculate the Mean:
Class Interval
fi
xi
fixi
1-4
6
2.5
15
4-7
30
5.5
165
7-10
40
8.5
340
10-13
16
11.5
184
13-16
4
14.5
51
16-19
4
17.5
70
Sum fi= 100
Sum fixi= 825
Mean = x̄ = ∑fixi/∑fi
Mean = 825/100 = 8.25
Therefore, mean = 8.25
7. The distributions of below give a weight of 30 students of a class. Find the median weight of a student.
Weight(in kg)
40-45
45-50
50-55
55-60
60-65
65-70
70-75
Number of students
2
3
8
6
6
3
2
Solution:
Class Interval
Frequency
Cumulative frequency
40-45
2
2
45-50
3
5
50-55
8
13
55-60
6
19
60-65
6
25
65-70
3
28
70-75
2
30
Given: n = 30 andn/2= 15
Median class = 55-60
l = 55, Cf= 13, f = 6 & h = 5
Median = 55+((15-13)/6)×5
Median=55 + (10/6) = 55+1.666
Median =56.67
Therefore, the median weight of the students = 56.67
Exercise 14.4
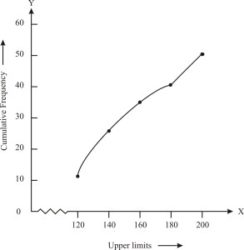
1. The following distribution gives the daily income of 50 workers if a factory. Convert the distribution above to a less than type cumulative frequency distribution and draw its ogive.
Daily income in Rupees
100-120
120-140
140-160
160-180
180-200
Number of workers
12
14
8
6
10
Solution
Convert the given distribution table to a less than type cumulative frequency distribution, and we get
Daily income
Frequency
Cumulative Frequency
Less than 120
12
12
Less than 140
14
26
Less than 160
8
34
Less than 180
6
40
Less than 200
10
50
From the table plot the points corresponding to the ordered pairs such as (120, 12), (140, 26), (160, 34), (180, 40) and (200, 50)on graph paper and the plotted points are joined to get a smooth curve and the obtained curve is known as less than type ogive curve
2.During the medical check-up of 35 students of a class, their weights were recorded asfollows:
Weight in kg
Number of students
Less than 38
0
Less than 40
3
Less than 42
5
Less than 44
9
Less than 46
14
Less than 48
28
Less than 50
32
Less than 52
35
Draw a less than type ogive for the given data. Hence obtain the median weight from the graph and verifythe result by using the formula.
Solution:
From the given data, to represent the table in the form of graph, choose the upper limits of the class intervals are in x-axis and frequencies on y-axis by choosing the convenient scale. Now plot the points corresponding to the ordered pairs given by (38, 0), (40, 3), (42, 5), (44, 9),(46, 14), (48, 28), (50, 32) and (52, 35)on a graph paper an join them to get a smooth curve. The curve obtained is known as less than type ogive.
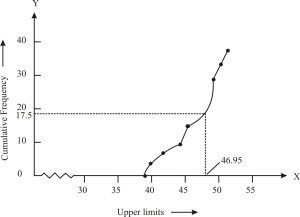
Locate the point 17.5 on the y-axis and draw a line parallelto the x-axis cutting the curve at a point. From the point, draw a perpendicular line to the x-axis. The intersection point perpendicular to x-axis is the median of the given data. Now, to find the mode by making a table.
Class interval
Number of students(Frequency)
Cumulative Frequency
Less than 38
0
0
Less than 40
3-0=3
3
Less than 42
5-3=2
5
Less than 44
9-5=4
9
Less than 46
14-9=5
14
Less than 48
28-14=14
28
Less than 50
32-28=4
32
Less than 52
35-22=3
35
The class 46 – 48 has the maximum frequency, therefore, this is modal class
Here,l= 46, h = 2,f1= 14,f0= 5 andf2= 4
The mode formula is given as:
Now, Mode =
= 46 + 0.95 = 46.95
Thus, mode is verified.
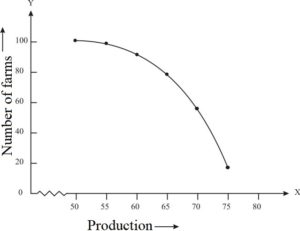
3. The following tables gives production yield per hectare of wheat of 100 farms of a village.
Production Yield
50-55
55-60
60-65
65-70
70-75
75-80
Number of farms
2
8
12
24
38
16
Change the distribution to a more than type distribution and draw its ogive.
Solution:
Converting the given distribution to a more than type distribution, we get
Production Yield (kg/ha)
Number of farms
More than or equal to 50
100
More than or equal to 55
100-2 = 98
More than or equal to 60
98-8= 90
More than or equal to 65
90-12=78
More than or equal to 70
78-24=54
More than or equal to 75
54-38 =16
From the table obtained draw the ogive by plotting the corresponding points where the upper limits in x-axis and the frequencies obtained in the y-axis are (50, 100), (55, 98), (60, 90), (65, 78), (70, 54) and (75, 16) on
this graph paper. The graph obtained is known as more than type ogive curve.