Class 10 Term 2 Standard Maths Solution [Series- PPQQA/1 Set 1, Paper Code- 30/1/1]
SECTION A
Question 1- Find the sum of first 30 terms of AP: -30, 24, -18,/..
Solution- a= -30, d= 6
= 15 [-60 + 29 (6)]
= 15 [-60+174]
= 15 [114]
= 1710
OR
Question 1- If an AP is Sn = n(4n+1), then find the AP
Solution- S1 = T1 = 5
S2= T1 + T2= 18
S2-S1 = T2= 13
AP= 5, 13, 21, 29, …
Question 2- A solid metallic sphere of radius 10.5 cm is melted and recast into a number of smaller cones, each of radius 3.5 cm and height 3 cm. Find the number of cones so formed.
Solution- r1 = 10.5 cm (sphere) and r2 (cone)= 3.5 cm, h2= 3cm
4/3πr³ = n x 1/3πr2² h
4r³ = nr2² h
4 x (105/10)³= n x 35/10 x 35/10 x 3
21 x 6= n
Number of cones formed= 126
Question 3 (a) Find the value of m for which the quadratic equation
(m-1) x² + 2(m-1)x + 1 = 0
Solution- D= 0
4 (m-1)² – 4(m-1) = 0
4 (m-1) [m-1-1]= 0
(m-1) (m-2)= 0
m= 2
(b) Solve the following quadratic equation for x: √3x² + 10x + 7√3= 0
Solution- √3x² + 3x + 7x + 7√3= 0
√3x (x+ √3) + 7 (x + √3)= 0
(x+ √3) [√3x + 7]= 0
x= √3 || x= -7/√3
Question 4- Find the mode of the following frequency distribution:
| Class | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| Frequency | 15 | 10 | 12 | 17 | 4 |
Solution- l= 40, f1= 17, f2= 4, fo= 12
Mode= l + f1-fo / 2f1 – fo- f2
= 40 + 17-12 / 34-12-4 x 10
= 40 + 5/18 x 10
= 40 + 25/9
= 40 + 2.78
= 42.78
Question 5- The product of Rehan’s age (in years) 5 years ago and his age 7 years from now, is one more than twice his present age. Find his present age.
Solution
| Past Age | Present Age | Future Age |
| x-5 | x | x+7 |
(x-5) (x+7) = 2x + 1
x² + 2x -35 = 2x+1
x² – 36 = 0
x² = 36
x= +_ 6
Present Age- 6 years
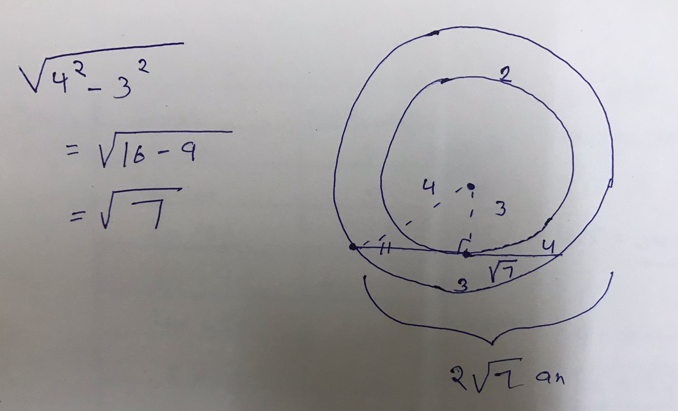
Question 6 Two concentric circles are of radii 4 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution-
SECTION B
Question 7- For what value of x, is the median of the following frequency distribution 34:5?
| Class | Frequency |
| 0-10 | 3 |
| 10-20 | 5 |
| 20-30 | 11 |
| 30-40 | 10 |
| 40-50 | x |
| 50-60 | 3 |
| 60-70 | 2 |
Solution-

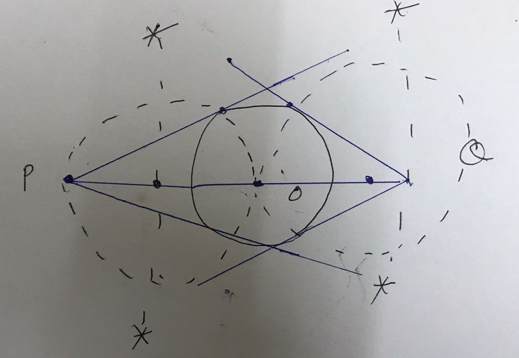
Question 8- Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Construct tangents to the circle from these two points P and Q.
Solution-
Question 9-(a) The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, then find the height of the building.
Solution-
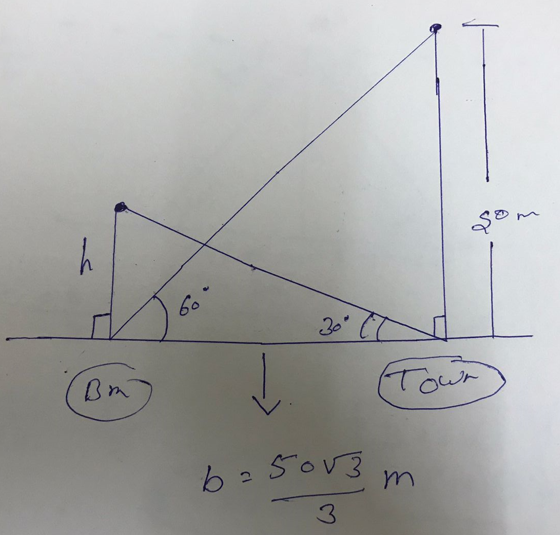
tan 60° = 50/b
b= 50/ tan 60°
b = 50/ √3
b= 50√3 / 3
tan 30° = h/(50√3/3)
h= 50√3/3 x 1/√3
= 50/3 m= 16.67 metres
OR
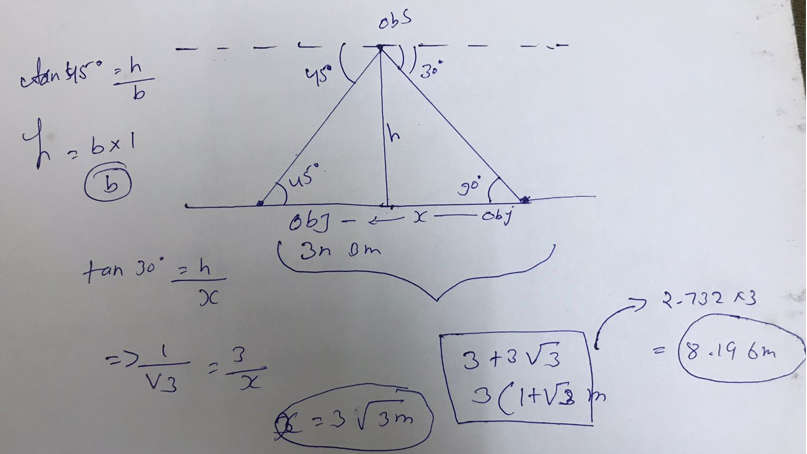
(b) From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks, then find the width of the river.
Solution-
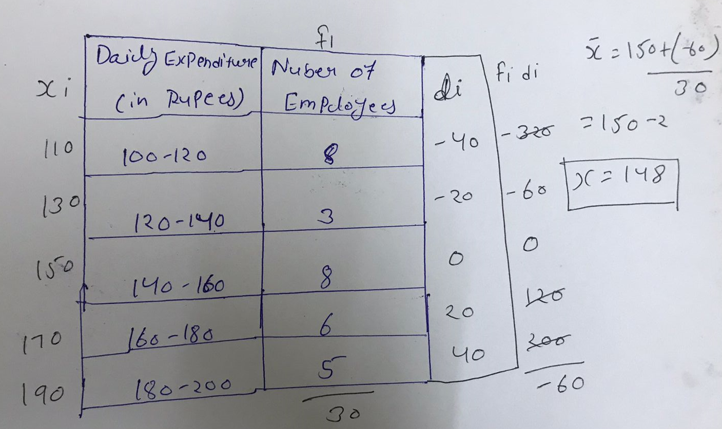
Question 10- Following is the daily expenditure on lunch by 30 employees of a company, Find the mean daily expenditure of the employees.
Solution
Question 11- From a solid cylinder of the height of 30 cm and radius of 7 cm, a conical cavity of height of 24 cm and same radius is hollowed out. Find the total surface area of the remaining solid.
Solution- H= 30 cm
R= 7 cm
Total Surface Area of Cylinder = Curved Surface Area of Cylinder + Curved Surface Area of Cone + πr²
TSA = 2 πrh + πrl + πr²
= πr (2h+ l+ r)
= 22/7 x 7 (60+25 + 7)
= 22 x 92
TSA= 2024 cm
OR