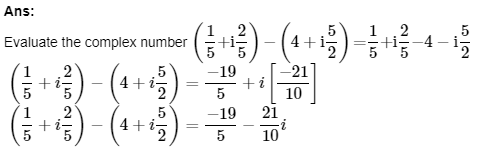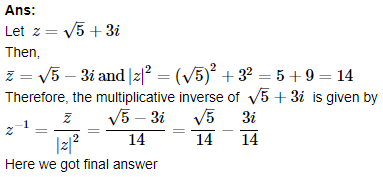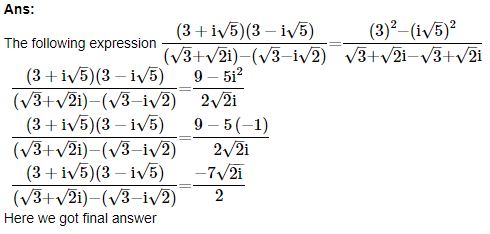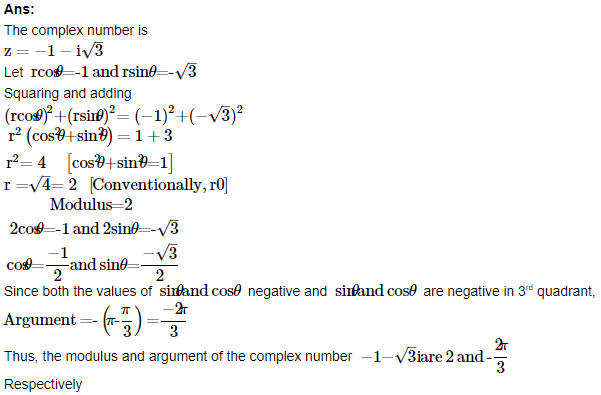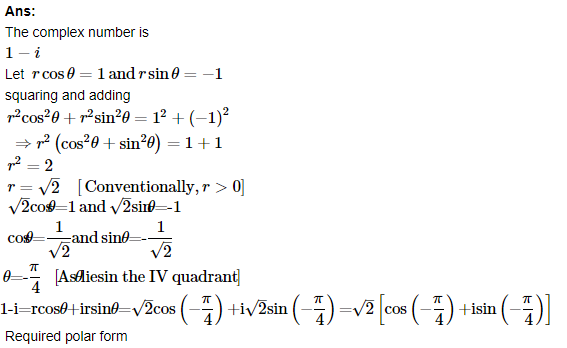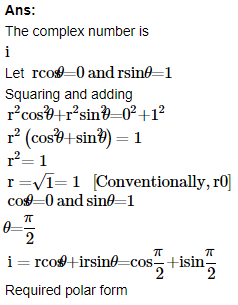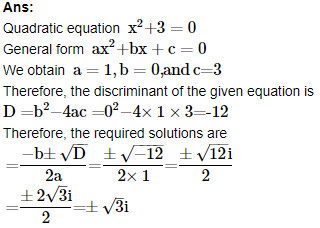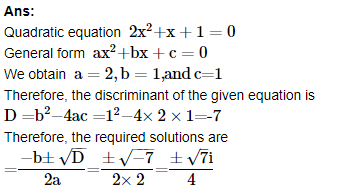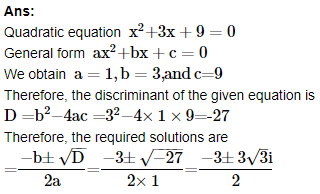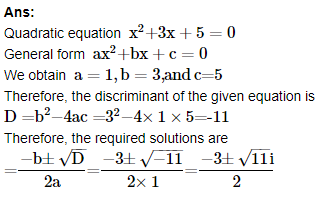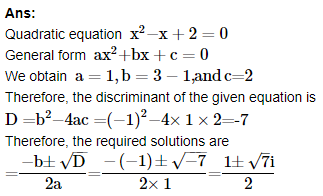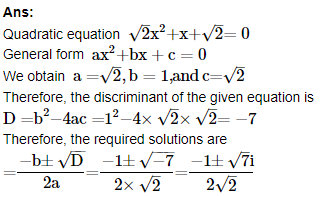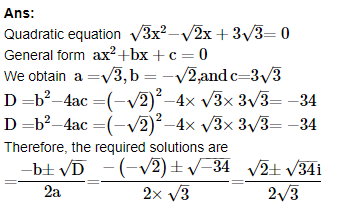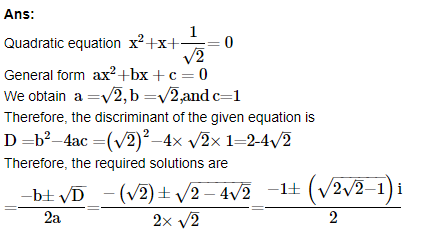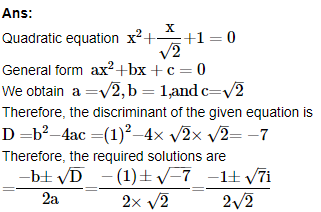Chapter 5 complex numbers and quadratic equations Questions and Answers: NCERT Solutions for Class 11th Maths

CBSE 10th Date sheet 2022      CBSE 12th Date Sheet 2022

Exercise 5.1

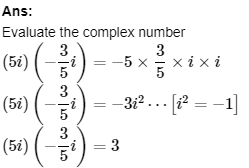
We get the final answer

---

2. Express the given complex number in the form a+ib:i9+i19

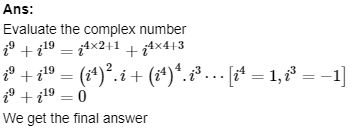
We get the final answer

---

3. Express the given complex number in the form a+ib:i−39

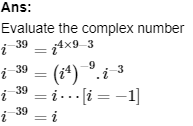
We get the final answer

---

4. Express the given complex number in the form a+ib:3(7+i7)+i(7+i7)

Ans: Evaluate the complex number 3(7+i7)+i(7+i7)=21+21i+7i+7i2 3(7+i7)+i(7+i7)=21+28i+7i2⋯[i2=−1] 3(7+i7)+i(7+i7)=14+28i We get the final answer

---

5. Express the given complex number in the form
a+ib:(1−i)−(−1+6i)

Ans: Evaluate the complex number (1−i)−(−1+6i)=1−i+1−i6 (1−i)−(−1+6i)=2−7i We get the final answer

---

---

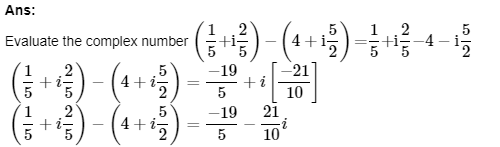
We get the final answer

---

7. Express the given complex number in the form

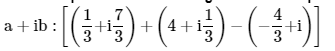
Ans: Evaluate the complex number

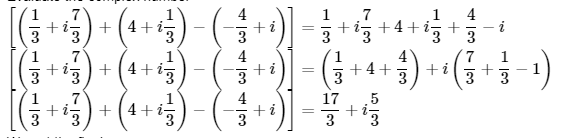
We get the final answer

---

8. Express the given complex number in the form a+ib:(1−i)4

Ans: Evaluate the complex number (1−i)4=[1+i2−2i]2 (1−i)4=[1−1−2i]2 (1−i)4=(−2i)×(−2i) (1−i)4=−4 We get the final answer

---

9. Express the given complex number in the form

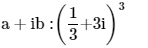
Ans: Evaluate the complex number

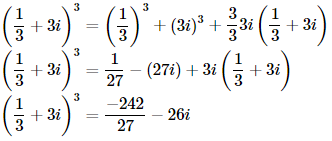
We get the final answer

---

10. Express the given complex number in the form

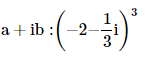
Ans: Evaluate the complex number

---

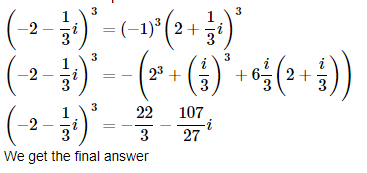
11. Find the multiplicative inverse of the complex number 4−3i

Ans: Let z=4−3i
Then, z¯¯¯=4+3i&|z¯¯¯|=42+(−3)2=16+9=25 Therefore, the multiplicative inverse of 4−3i is given by z−1=z¯¯¯|z|2=4+3i25=425+325i Here we got final answe

---

12. Find the multiplicative inverse of the complex number 5–√+3i

---

13. Find the multiplicative inverse of the complex number −i

Ans: Let z=−i Then, z¯=i and| z| 2=12=1 Therefore, the multiplicative inverse of −i is given by z−1=z¯| z| 2=i1=i Here we got final answer

---

14. Express the following expression in the form of

---

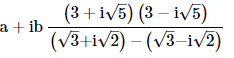
Exercise 5.2

---

1. Find the modulus and the argument of the complex number z=−1−i3–√

---

2. Find the modulus and the argument of the complex number z=−3–√+i

---

3. Convert the given complex number in polar form 1−i

---

4. Convert the given complex number in polar form −1+i

---

5. Convert the given complex number in polar form −1−i

---

6. Convert the given complex number in polar form −3

---

7. Convert the given complex number in polar form 3–√+i

---

8. Convert the given complex number in polar form i

---

Exercise 5.3

---

1. Solve the equation x2+3=0

---

2. Solve the equation 2x2+x+1=0

---

3. Solve the equation x2+3x+9=0

---

4. Solve the equation −x2+x−2=0

---

5. Solve the equation x2+3x+5=0

---

6. Solve the equation x2−x+2=0

---

7. Solve the equation 2–√x2+x+2–√=0

---

8. Solve the equation 3–√x2−2–√x+33–√=0

---

9. Solve the equation

---

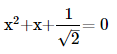
10. Solve the equation

---

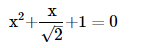
Last Updated on: nov 01, 2022