Chapter 10 Mechanical Properties of Fluids Questions and Answers: NCERT Solutions for Class 11th Physics (Partnership Physics )

CBSE 10th Date sheet 2022      CBSE 12th Date Sheet 2022

Class 11th Physics (Partnership Physics ) NCERT book solutions for Chapter 10 Mechanical Properties of Fluids Questions and Answers.

---

1. Explain why (a) The blood pressure in humans is greater at the feet than at the brain

Ans: The pressure of a liquid with densityρ
, with the liquid column of h
is given by the relation:
P= ρhg
here g
is the acceleration due to the gravity
It can be inferred that pressure is directly proportional to height. In the case of humans, the circulatory system can be considered as the liquid (blood)-column.
The height of the column is the least at the head level and the maximum at the feet; hence, the pressure (blood pressure) in human vessels depends on this height. Thus, the blood pressure at the feet is more than what it is at the brain.
(b) Atmospheric pressure at the height of about 6km
decreases to nearly half of its value at the sea level, though the height of the atmosphere is more than 100km
Ans: The density of a fluid depends on how much it has been pressed by the amount of fluid over it. This means that the density of air is the maximum near the sea level.
The density of air increases with a decrease in the height from the sea surface. At the height of about 6 km, the total mass squeezes the layer of air over here to nearly half of the pressure value at sea level.
In the case of just small changes in altitude, the atmospheric pressure is proportional to density. However, when larger height scales are considered, the density itself depends on the height, and the pressure isn't linearly dependent anymore.
Moreover, the pressure increases faster than the linear dependence expected in the case of small changes in altitudes.
(c) Hydrostatic pressure is a scalar quantity even though pressure is force divided by area.
Ans: Mathematically, pressure is the perpendicular force per unit area.
So, only the force component that is perpendicular to the surface or along the area vector is used. The direction of this component and the direction of the area vector are the same.
Hence effectively, there is no direction involved anymore.
In other words, when force is applied to a liquid, the pressure in the liquid is transferred in all directions. Thus, the hydrostatic pressure does not have a fixed direction, and it is a scalar physical quantity.

---

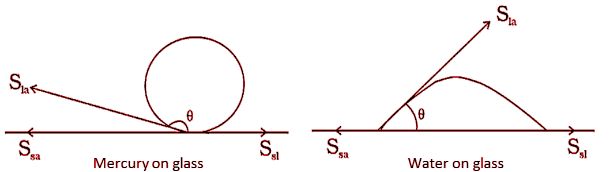
2. Explain why (a) The angle of contact of mercury with glass is obtuse, while that of water with glass is acute

Ans: The angle between the surface inside the liquid and the tangent to the liquid surface at the point of contact is the angle of contact(θ) , as shown in the following figure

Let Sla
be the interfacial tension at the liquid-air interface, Ssl
be at the solid-liquid interface, and Ssa
be at the solid-air interface. At all the points of contact, the surface forces between the three media must be in equilibrium, i.e.,
cosθ=Ssa−SslSla
In the case of a mercury drop on glass, Ssl>Ssa
, the angle of contact (θ)
is obtuse.
In the case of water on the glass,Ssl is acute.
(b) Water on a clean glass surface tends to spread out, while mercury on the same surface tends to form drops. (Put differently, water wets glass while mercury does not.)
Ans: The Mercury molecules have a strong force of attraction between themselves and a weak force of attraction toward solids. Hence, the angle of contact tends to become obtuse, and the molecules come closer and tend to form a drop. While in the case of water, the ratio of attraction between water molecules and the attraction between water molecules and the glass is lower. Hence the water molecules stay closer to glass molecules as well, keeping the glass surface wet.
(c) The surface tension of a liquid is independent of the area of the surface
Ans: Surface tension can be defined as the force acting per unit length at the interface between the liquid and any other material.
There is no dependency of this force on the area of the surface.
Hence, surface tension is independent of the area of the surface of the liquid.
(d) Water with detergent dissolved in it should have small angles of contact.
Ans: Detergent water has small angles of contact (θ)
because the detergent molecules are sticky; in other words, they are significantly attracted to the water molecules and the solid which is in contact with the detergent water.
Therefore, the molecules of water can get closer to the solid.
In other words, Ssl and the value of cosθ=Ssa−SslSla
increases, leading to a decrease in the value of θ
making it acute or small.
(e) A drop of liquid under no external forces is always spherical in shape
Ans: Surface tension pulls the surface together as much as possible.
This means that in the absence of any other external force/pressure. The surface tension will try to shrink the area as much as possible.
Beyond a certain extent, the volume cannot be shrunk, and the shape with minimum surface area for the unchanged volume is a sphere.
Hence a droplet will tend to become spherical.

---

3. Fill in the blanks using the word(s) from the list appended with each statement: (a) Surface tension of liquids generally ……with temperatures (increases / decreases

Ans: decreases. The surface tension of a liquid surface is inversely proportional to the motion of the liquid molecules. An increase in the temperature leads to an increase in the random motion of the molecules, and hence the surface tension drops.
(b) Viscosity of gases…… with temperature, whereas viscosity of liquids …… with temperature (increases / decreases) Ans: increases; decreases
All fluids experience resistance to their motion when they are made to flow. This resistance is known as viscosity.
The motion of the gas molecules becomes very random, and giving them a direction gets difficult.
The viscosity of gases increases with the increasing random motion of the molecules. The molecules of the liquid are more restricted than and not as free as those of gas. Increasing the temperature of liquids increases the motion of the molecules, making them more mobile and improves their ability to flow.
Hence the viscosity decreases with an increase in temperature.
(c) For solids with elastic modulus of rigidity, the shearing force is proportional to….., while for fluids it is proportional to ……(shear strain / rate of shear strain)
Ans: Shear strain; Rate of shear strain
For elastic solids, shearing force is proportional to the shear strain.
However, the shearing force is proportional to the rate of shear strain in the case of fluids.
(d) For a fluid in a steady flow, the increase in flow speed at a constriction follows……. (conservation of mass / Bernoulli's principle)
Ans: Conservation of mass/Bernoulli’s principle
Bernoulli's principle works in the conservation of mass and energy, which includes the effects of the continuity equation. Hence, Conservation of mass and Bernoulli's Equation is the correct options
(e) For the model of a plane in a wind tunnel, turbulence occurs at a …... speed for turbulence for an actual plane (greater / smaller)
Ans: Greater
As provided in the question, there is a model of a plane in a wind tunnel. Following Bernoulli's Principle and referring to the relevant Reynolds number it can be seen that the turbulence occurs at a greater speed.

---

4. Explain why
(a) To keep a piece of paper horizontal, you should blow over, not under, it

Ans: As per Bernoulli's principle, the fluid pressure reduces if the velocity is increased.
The paper falls under gravity, and to make it stay up and horizontal, we need to reduce the pressure on the top of it. For this reason. one should blow on the upper side of the paper.
(b) When we try to close a water tap with our fingers, fast jets of water gush through the openings between our fingers
Ans: According to the continuity equation, for a flowing fluid, the rate of volume of fluid crossing any cross-section is constant. This means that the velocity of the flowing fluid is high if the cross-section of the passage is reduced.
Covering the tap opening reduces the cross-section, and hence the water gushes out with a lot of speed.
(c) The size of the needle of a syringe controls flow rate better than the thumb pressure exerted by a doctor while administering an injection
Ans: The liquid velocity at the needle is much higher than that inside the syringe. And higher velocity means much lower pressure.
Furthermore, the changes in the pressures at the different cross-sections are proportional to the pressures in the regions. A human thumb cannot constantly provide constant pressure. So the significant change in the pressures is carried to the needle end as well. The pressure over here changes proportionally.
But as mentioned before, the changes in the pressure at the needle end are proportional to the pressure at the needle end, which is very small.
Hence the absolute change in the pressure at the needle end is also minimal. Thus it can be said that the consistency of the pressure is controlled by the cross-section of the needle.
(d) A fluid flowing out of a small hole in a vessel results in a backward thrust on the vessel
Ans: As the fluid flows out of a small orifice, its velocity is significantly high according to the continuity equation.
This outgoing liquid generates momentum.
Going by the law of conservation of momentum, a counter momentum is generated on the vessel, making it experience a backward thrust.
(e) A spinning cricket ball in air does not follow a parabolic trajectory
Ans: A thrown spinning cricket ball has two motions – rotational and linear. The falling ball experiences viscosity in the upwards direction.
A rotating ball experiences viscosity due to the relative motion of the surface of the ball and the air in the vicinity. So at any instance, the face that is moving downwards faces an upwards viscosity force while the face going upwards faces a downwards viscosity force.
These viscous forces add up in such a way that the velocity of the air on one side of the ball is much higher than on their side, reducing the pressure on the side which has a higher velocity.
This pressure imbalance causes a force directed towards the low-pressure region. Hence the ball deviates from the expected parabolic trajectory.

---

5. A 50kg girl wearing high heel shoes balances on a single heel. The heel is circular with a diameter 1.0cm . What is the pressure exerted by the heel on the horizontal floor?

Ans: As provided, the mass of the girl, m = 50 kg
, the diameter of the heel d = 1 cm = 0.01 m
, the radius of the heel, r=d2=0.005m
Therefore, the area of the heel, A=πr2
⇒A=π×0.0052
⇒A=7.85×10−5m2
The force exerted by the heel on the floor is:
F = mg = 50 × 9.8 =490 N
The pressure exerted on the floor by the heel:
P=FA=4907.85×10−5=6.24×106Nm−2
Hence clearly, the pressure exerted by the heel on the horizontal floor is 6.24×106Nm−2

---

6. Torricelli's barometer used mercury. Pascal duplicated it using French wine of density 984kg/m3 . Determine the height of the wine column for normal atmospheric pressure.

Ans: Provided that,
Density of mercury, ρ1=13.6×103kg/m3
The height of the mercury column,
h1=0.76m
Provided density of French wine,
ρ2=0.984×103kg/m3
Let the height of the column of wine =h2
The acceleration due to gravity=g=9.8ms−2
The pressure in both the columns (given byρhg
) is equal at equal altitudes of the same liquid, which means:
ρ1h1g1=ρ2h2g2
⇒h2=ρ1h1gρ2g=10.5m
Thus, the height of the column of wine at normal atmospheric pressure is 10.5m

---

7. A vertical off-shore structure is built to withstand a maximum stress of 109Pa . Is the structure suitable for putting up on top of an oil well in the ocean? Take the depth of the ocean to be roughly 3km , and ignore ocean currents

Ans: Yes
As provided, the maximum allowable stress for the structure, P=109Pa
Depth of the ocean, d=3×103m
The density of water, ρ=103kg/m3
The acceleration due to gravity, g=9.8m/s2
The pressure exerted because of water at depth,
P=ρdg=3×103×103×9.8=2.94×107Pa
Hence it has been calculated that the maximum allowable stress for the structure is significantly greater than the pressure of the water and hence can be used safely.

---

8. A hydraulic automobile lift is designed to lift cars with a maximum mass of 3000kg
. The area of cross-section of the piston carrying the load is 425cm2
. What maximum pressure would the smaller piston have to bear?

Ans: As provided, the mass limit on the mass of a car that can be lifted, m = 3000 kg
The area of cross-section of the load-carrying piston, A=0.0425m2
The maximum force exerted by the load, F = mg = 3000 × 9.8 = 29400 N
The maximum pressure experienced by the piston that is carrying the load is, P=FA=29400425×10−4= 6.917 ×10−4 Pa
Since the pressure is transferred/transmitted equally in all directions in a liquid, the maximum pressure on the smaller piston would be 6.917 ×10−4 Pa

---

9. A U-tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are in level with 10.0cm
of water in one arm and 12.5cm
of spirit in the other. What is the specific gravity of spirit?

Ans: The provided system of water, mercury, and methylated spirit can be shown as follows:

The height of the spirit column, h1=12.5cm=0.125m
The height of the water column is: h2=10cm=0.1m
P0=
Atmospheric pressure, ρ1=
Density of spirit, ρ2=
Density of water
Pressure at point A, P0+ρ1h1g
Pressure at point B, P0+ρ2h2g
The values of pressures at points A and B are equal
P0+ρ1h1g=P0+ρ2h2g
⇒ρ1ρ2=h2h1=0.8
Hence, clearly, the specific gravity of spirit is 0.8

---

10. In problem 10.9, if 15.0cm of water and spirit each are further poured into the respective arms of the tube, what is the difference in the levels of mercury in the two arms? (Specific gravity of mercury = 13.6 )

Ans: Provided that,
Height of the water column, h1=10+15=25cm
Height of the spirit column, h2=12.5+15=27.5cm
The density of water, ρ1=1gcm−3
; that of spirit, ρ2=0.8gcm−3
and that of mercury is 13.6gcm−3
Now, let h
be the difference between the levels of mercury in the two arms. The pressure exerted by the height h
of the mercury column: =ρhg=h×13.6
The difference between the pressures exerted by water and spirit: ρ1h1g−ρ2h2g=g(25×1 27.5×0.8)=3g
Equating the pressures, we get:
13.6 hg = 3g
⇒h = 0.220588 ≈ 0.221 cm
The difference between the levels of mercury in the two arms is 0.221 cm

---

11. Can Bernoulli's equation be used to describe the flow of water through a rapid in a river? Explain.

Ans: Bernoulli's equation cannot describe the turbulent flow of fluids like that in a rapid river. Water flow in a river is chaotic. Bernoulli's equation suggests that an increase in a fluid's velocity occurs concurrently with a decrease in static pressure or simultaneously with a reduction in potential energy throughout the water flow.
This theory is only applicable to isentropic flows, wherein turbulence and other disturbances are ignored.
There are various versions of Bernoulli's equation with respect to various flow kinds. For instance, incompressible flows obey the simple form of Bernoulli's equation whereas compressible flows obey an advanced form of the equation.
Bernoulli's theory is in accordance with the principle of energy conservation. Clearly, at each point on the flowing water in the river, the sum of any and all sources of energy is equal to that as in a steady flow. The sum for kinetic energy, internal energy and potential energy should also maintain stability.

---

12. Does it matter if one uses gauge instead of absolute pressures in applying Bernoulli's equation? Explain.

Ans: Gauge pressure gives us the pressure difference in the fluid under consideration and some standard pressure. Using gauge pressure will only tell us about the pressure difference.
Bernoulli's principle assumes that the pressures under consideration are linearly proportional to the square of the velocity and the height of the fluid.
However, the difference in pressure cannot be directly shown to have this proportionality. Hence, we need to convert the gauge pressure to absolute pressure before plugging it into Bernoulli's equation.
So yes, it matters if we use gauge instead of absolute pressures in applying Bernoulli's equation.

---

13. Glycerin flows steadily through a horizontal tube of length 1.5m and radius1.0cm
. If the amount of glycerin collected per second at one end is4.0×10−3kg/s , what is the pressure difference between the two ends of the tube? (Density of glycerin 1.3×103kg/m3 and viscosity of glycerin=0.83Pas ). (You may also like to check if the assumption of laminar flow in the tube is correct).

Ans: Provided that,
Length of the horizontal tube, l=1.5 m
The radius of the tube, r=1cm=0.01m
Thus, the diameter of the tube, ∴d=0.02m
As given in the question, Glycerine is flowing at a rate of M=4.0×10−3kgs−1
The density of Glycerine, ρ=1.3×103kgm−3
Viscosity of Glycerineη=0.83 Pa s
The volume of Glycerine flowing per sec:
V=M/ρ=4.0×10−31.3×103=3.08×10−6m3s−1
According to Poiseuille's Law, we have the expression for the rate of flow:
V=πPr48ηl
here, P is the pressure difference between the two ends of the tube
P=V8ηlπr4= 9.8 × 102Pa
Reynolds' number is given by the following expression:
4ρVπdη=4(1.3×103)(3.08×10−6)π(0.02)0.83=0.3
Reynolds' number is about 0.3
; therefore, the flow is laminar.

---

14. In a test experiment on a model aero plane in a wind tunnel, the flow speeds on the upper and lower surfaces of the wing are 70m/s and 63m/s respectively. What is the lift on the wing if its area is2.5m2 ? Take the density of air to be1.3kgm−3

Ans: The given speed of wind on the wing's upper surface, and the speed of wind relative to the wing's lower surface v2=63m s−1
The area of the wing, A=2.5m2
The density of air, ρ=1.3kg/m3
Now, according to Bernoulli's theorem, we have the relation: P1+12ρv12=P2+12ρv22
In the current case, let P2
be the pressure on the lower side of the wing and P1
be the pressure on the upper side, and the v-s are the velocities mentioned initially.
The required lift is the force that comes from the pressure difference in the lower and the upper surface.
This can be obtained as:
Lift=(P1−P2)A=(12ρv22−12ρv12)A
Lift=12ρ(v22−v12)A=121.3(702−632)2.5=1.51×103N
Hence, 1.51×103N
is the lift on the wing of the airplane.

---

15. Figures (a) and (b) refer to the steady flow of a (non-viscous) liquid. Which of the two figures is incorrect? Why?

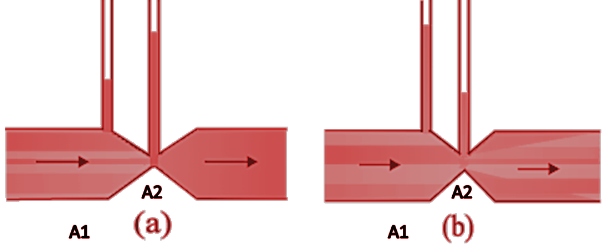
Ans: Considering the second figure: Let us say A1 and A2 are the cross-section areas of the pipe and the narrow region, respectively and V1 and V2 are the speeds of the fluid in the normal region of the pipe and at the narrow region, respectively
According to the law of continuity: A1×V1=A2×V2
Hence it can be noted that the velocity of the liquid at the narrow region is higher than that in the normal region.
Now using Bernoulli's theorem, it can be said that the pressure is high in a region where the velocity is low. Hence the pressure at the normally thick (at A1) will be higher than that at A2.
Hence the column connected at this place will also have higher pressure at the point of contact. This is why the liquid column will also rise higher than the column connected at the narrow junction. Therefore, figure (b) is possible.

---

16. The cylindrical tube of a spray pump has a cross-section of 8.0cm2 one end of which has 40 fine holes each of diameter1.0mm . If the liquid flow inside the tube is1.5mmin−1 , what is the speed of ejection of the liquid through the holes?

Ans: Provided that,
Area of the cross-section of the spray pump A1=8×10−4m2
Number of holes, n = 40
Diameter of each hole, d=10−3m
The radius of each hole, r=0.5×10−3m
Area of the cross-section of each hole, a=πr2=π(0.5×10−3)2
The total area of 40 holes, A=na=nπr2=31.41×10−6m2
The speed of flow of liquid inside the tube, v1=1.5m/min=0.025m/s
The liquid is ejected through the holes at the speed of v2
According to the continuity equation, we have v2=A1v1A2=0.633 m/s
Therefore, it has been calculated that the speed of ejection of the liquid through the holes is 0.633 m/s.

---

17. A U-shaped wire is dipped in a soap solution, and removed. The thin soap film formed between the wire and the light slider supports a weight of 1.5×10−2N . (Which includes the small weight of the slider). The length of the slider is30cm . What is the surface tension of the film?

Ans: The weight that the soap film supports, W=1.5×10−2N
Length of the slider, l=0.3m
A soap film has two free surfaces.
Therefore, the total length =2l=0.6m
Hence the surface tension is obtained as
S=Force2l=1.5×10−2N0.6m=2.5×10−2N/m
Therefore, the surface tension of the film is obtained as2.5×10−2N/m

---

18. Figure 10.24 (a) shows a thin liquid film supporting a small weight4.5×10−2N . What is the weight supported by a film of the same liquid at the same temperature in Fig. (b) and (c)? Explain your answer physically a) Equal stresses

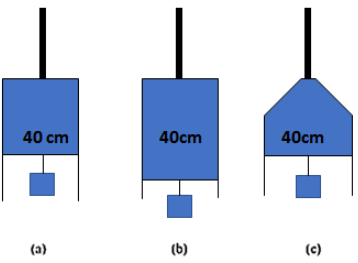
Ans: For case (a):
The length of the liquid film is supported by the weight l = 40 cm = 0.4 m
The weight supported by the film, W=4.5×10−2N
Every liquid film has two free surfaces. Hence the surface tension can be calculated as
S=Force2l=4.5×10−2N2×0.4m=5.625×10−2N/m
Since the properties of the liquid are the same in all the cases., the surface tension in all three cases is equal. And the weight supported is also the same in all three cases, i.e., =5.625×10−2N/m

---

19. What is the pressure inside the drop of mercury of radius 3.0mm at room temperature? Surface tension of mercury at that temperature (20∘C) is 4.65×10−1Nm−1 . The atmospheric pressure 1.01×105Pa . Also give the excess pressure inside the drop.

Ans: As provided, the radius of the mercury drop, r=3×10−3m
The surface tension of mercury, S=4.65×10−1N/m
The atmospheric pressure, P0=1.01×105Pa
Total pressure inside the mercury drop = Excess pressure inside mercury + Atmospheric pressure
Total pressure =2Sr+P0=2×4.65×10−13×10−3+1.01×105=1.013×105Pa
Hence the excess pressure is obtained as =2Sr=310Pa

---

20. What is the excess pressure inside a bubble of soap solution of radius5.0mm , given that the surface tension of soap solution at the temperature (20∘C) is 4.65×10−1Nm−1 . If an air bubble of the same dimension were formed at the depth of 40.0cm inside a container containing the soap solution (of relative density1.20 ), what would be the pressure inside the bubble? (1 atmospheric pressure is 1.01×105Pa .

Ans: As provided in the question, the excess pressure inside the soap bubble is 20 P;
The pressure inside the air bubble is =1.06×105Pa
A soap bubble is of radius, r=5×10−3m
The surface tension of the soap solution, S=2.5×10−2N/m
Also, the relative density of the soap solution = 1.20
Thus, the density of the soap solution, ρ=1.2×ρair=1.2×103kg/m2
It is given that the air bubble is formed at a depth, h = 40 cm = 0.4 m
The radius of the air bubble, r=5×10−3m
Acceleration due to gravity, g=9.8m/s2
Therefore, it can be noted that the excess pressure inside the soap bubble is given by:
P=4Sr=20Pa
The excess pressure inside the air bubble can be written as:
P=2Sr=10Pa
The total pressure inside the air bubble under consideration is the sum of the atmospheric pressure, the pressure due to the column of the liquid and the excess pressure:
Ptotal=P0+hgρ+P=1.057×105Pa
Hence, the pressure inside the air bubble is 1.057×105Pa

---

21. A tank with a square base of area 1.0m2 is divided by a vertical partition in the middle. The bottom of the partition has a small-hinged door of area 20.0cm2 . The tank is filled with water in one compartment, and an acid (of relative density 1.7) in the other, both to a height of. compute the force necessary to keep the door closed.4.0m

Ans: Provided that,
Base area of the given tank,A=1.0m2
Area of the hinged door, a=0.02m2
The density of water, ρ1=103kgm−3
The density of acid, ρ2=1.7×103kgm−3
Height of the water column, h1=4m
Height of the acid column, h2=4m
Acceleration due to gravity, g=9.8m/s2
Now, the pressure due to water is given as: P1=ρ1h1g=4×103×9.8=3.92×104Pa
The pressure due to acid is given as: P2=ρ2h2g=4×1.7×103×9.8=6.662×104Pa
The pressure difference between the two columns: ΔP=P2−P1=2.744×104Pa
Thus, the force exerted on the door F=P×a=54.88N
It can be concluded that the force necessary to keep the door closed is 54.88N

---

22. A manometer reads the pressure of a gas in an enclosure as shown in figure When a pump removes some of the gas, the manometer reads as in figure (b) The liquid used in the manometers is mercury and the atmospheric pressure is 76 cm of mercury

---

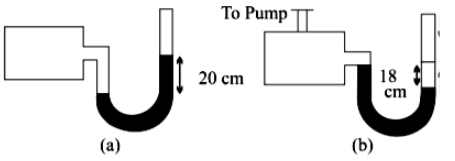
(a) Give the absolute and gauge pressure of the gas in the enclosure for cases (a) and (b), in units of cm of mercury.
Ans: In the first case i.e., fig (a)
Atmospheric pressure, P0=76cmHg
The pressure (or height) difference between the levels of mercury in the two limbs denotes the gauge pressure.
Hence, the gauge pressure is 20 cm of Hg.
Pabsolute = P0 + PGauge = 76 + 20 = 96 cm Hg
In the second figure (figure (b)), the difference between the levels of mercury in the two limbs = 18 cm Hence, gauge pressure is = 18 cm Hg.
Again, the Pabsolute = P0 + PGauge = 76 + (-18) = 58 cm Hg
(b) How would the levels change in case (b) if 13.6 cm of water (immiscible with mercury) are poured into the right limb of the manometer? (Ignore the small change in the volume of the gas).
Ans: Now, 13.6cm
water is filled into the right limb of figure (b).
The relative density of mercury 13.6cm
In other words, a column of 13.6cm
water is equivalent to 1cm
mercury.
Consider h
being the difference in the mercury levels in the two limbs.
The pressure experienced in the right limb is given as:
Pright = P0 + 1cmHg = 76 + 1 = 77 cm Hg
The level of the mercury column will go up in the left limb.
Hence, pressure in the left limb, PL=58+h
Equating the pressures in both the limbs and simplifying for h, we get:
77=58+h
⇒h=19cm It can be hence concluded that the mercury levels differ by 19cm .

---

23. Two vessels have the same base area but different shapes. The first vessel takes twice the volume of water that the second vessel requires to fill up to a particular common height. Is the force exerted by the water on the base of the vessel the same in the two cases? If so, why do the vessels filled with water to that same height give different readings on a weighing scale?

Ans: Yes,
Pressure in a liquid is given as:
P=ρhg
. The heights up to which the vessels are filled are equal, the densities are equal, and g is the same for both cases. Hence the pressures are also the same
Now, let the force that is experienced at the base of an area A be F=P×A
Therefore, the forces in both cases are equal.

---

24. During blood transfusion the needle is inserted in a vein where the gauge pressure is 2000Pa . At what height must the blood container be placed so that blood may just enter the vein? (Use the density of whole blood from Table 10.1).

Ans: The given gauge pressure, P = 2000 Pa
The density of whole blood, ρ=1.06×103kgm−3
Let h
be the height of the blood container
The pressure inside the blood container is P=ρhg
Here g=9.8m/s2
is the acceleration due to gravity,
⇒h=Pgρ=20009.8×1.06×103=0.1925m
This means that the blood would enter the vein only if the container is kept at a height of 0.1925m higher than the height at which the needle is inserted.

---

25. In deriving Bernoulli's equation, we equated the work done on the fluid in the tube to its change in the potential and kinetic energy.
(a) What is the largest average velocity of blood flow in an artery of diameter 2.0×10−3m if the flow must remain laminar?

Ans: The diameter of the given artery, d=2×10−3m
The viscosity of blood, η=2.084×10−3Pas
The density of blood, ρ=1.06×103kg/m2
Reynolds' number for laminar flow, NR = 2000
The maximum average velocity of blood flowing through the d-diameter orifice is as follows:
V=NRηρd=2000×2.084×10−3(1.06×103)(2×10−3)=1.966m/s
Therefore, the largest average velocity of blood is 1.966m/s
(b) Do the dissipative forces become more important as the fluid velocity increases? Discuss qualitatively.
Ans: The dissipative forces become more prominent with an increase in the fluid velocity. As the velocity increases, the turbulence also increases. The turbulent nature of the flow causes dissipative loss in a fluid. .

---

26.(a) What is the largest average velocity of blood flow in an artery of radius 2.0×10−3m if the flow must remain laminar?

Ans: Provided that,
Radius of the artery, r=2×10−3m
Diameter of the artery, d=2(2×10−3m)
The viscosity of blood, η=2.084×10−3Pas
The density of blood, ρ=1.06×103kg/m2
The Reynolds number of Laminar flow, NR = 2000
The largest value of average velocity can be given as:
V=NRηρd=2000×2.084×10−3(1.06×103)(4×10−3)=0.983m/s
Hence the largest average velocity of blood flow in an artery of the radius2×10−3m is 0.983m/s
(b) What is the corresponding flow rate? (Take viscosity of blood to be 2.084×10−3Pas ).
Ans: The flow rate is written as the time derivative of the volume that flowed past a cross-section:
R=πr2VAvg=3.14(2×10−3)2(9.83)=1.235×10−5m3/s
Hence the corresponding flow rate is 1.235×10−5m3/s

---

27. A plane is in level flight at a constant speed and each of its two wings has an area of 25m2 . If the speed of the air is 180km/h over the lower wing and 234km/h over the upper wing surface, determine the plane's mass. (Take air density to be1kg/m3 ).

Ans: As provided in the question, the area of the wings is A=2×25=50m2
Speed of air over the lower wing, v1=180km/h=50m/s
Speed of air over the upper wing, v2=234km/h=65m/s
The density of air, ρ=1kg/m3
The pressure of air over the lower wing=P1
The pressure of air over the upper wing =P2
The upward force on the plane can be obtained using Bernoulli's equation as: P1+12ρv12=P2+12ρv22
Thus, the upward force is obtained as:
Lift=(P1−P2)A=(12ρv22−12ρv12)A=43125N
The mass of the plane can be obtained as:
m=F/g=4400.5kg
Hence, the mass of the plane is nearly 4400.5kg

---

28. In Millikan's oil drop experiment, what is the terminal speed of an uncharged drop of radius 2.0×10−5m and density1.2×103kg/m3 . Take the viscosity of air at the temperature of the experiment to be 1.8×10−5Pas . How much is the viscous force on the drop at that speed? Neglect buoyancy of the drop due to air.

Ans: The given terminal speed =5.8cm/s , the viscous force =3.9×10−10N
The radius of the given uncharged drop, r=2.0×10−5m
The density of the uncharged drop, ρ=1.2×103kgm−3
It is known that the viscosity of air, η=1.8×10−5Pas
In this case, the density of air (ρ0
) can be taken as zero to neglect buoyancy of air. Acceleration due to gravity is g=9.8m/s2
Terminal velocity (v) is given as:
v=2r2(ρ−ρ0)g9η=2(2.0×10−5)2(1.2×103−0)9.891.8×10−5=5.8×10−2m/s
Hence, the terminal velocity of the drop is 5.8cm/s
The viscous force experienced by the drop is given by:
F=6πηrv
⇒F=3.9×10−10N
Hence the viscous force is calculated to be 3.9×10−10N

---

29. Mercury has an angle of contact equal to 140∘ with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside? Surface tension of mercury at the temperature of the experiment is 4.65×10−1Nm−1 . Density of mercury is 13.6×103kg/m3

Ans: As provided in the question, the angle of contact between mercury and soda-lime glass, θ=140∘
The radius of the narrow tube r=1.0×10−3m
The given surface tension of mercury, S=0465N/m
The density of mercury, ρ=13.6×103kgm−3
Dip in the height of the mercury =h
Acceleration due to gravity, g=9.8m/s2
The surface tension can be written in terms of the angle of contact and the dip in height:
S=hρgr2cosθ
⇒h=2cosθSρgr=−0.00534m=−5.34mm
Notice the negative sign; it shows the dropping level of mercury.
Hence, the mercury level drops by 5.34 mm.

---

30. Two narrow bores of diameters 3.0 mm and 6.0 mm are joined together to form a U-tube open at both ends. If the U-tube contains water, what is the difference in its levels in the two limbs of the tube? Surface tension of water at the temperature of the experiment is 7.31×10−2Nm−1 . Let the angle of contact to be zero and density of water be 1.0×103kg/m3

Ans: Provided that,
Diameter of the first bore, d1=3.0×10−3m
Hence the radius of the first bore, r1=d1/2=1.5×10−3m
Diameter of the second bore, d2=6.0×10−3m
Hence, the radius of the second bore, r2=d2/2=3.0×10−3m
The surface tension of water, S=7.3×10−2N/m
The angle of contact between the water surface and the bore surface, θ=0∘
The density of water, ρ=1.0×103kgm−3
Acceleration due to gravity, g=9.8m/s2
Leth1
and h2
be the heights to which water rises in the first and second tubes, respectively. These are given as:
h1=2Scosθρgr1
and h2=2Scosθρgr2
The difference in the water levels in the two limbs of the tube can be calculated as:
Δh=2Scosθρgr1−2Scosθρgr2=2×7.3×10−2×cos01.0×103×9.8=4.97mm
Hence, the difference between the levels is obtained as =4.97mm

---

31.(a) It is known that density ρ of air decreases with height y as ρ0ey/y0 . Where ρ0=1.25kgm−3 the density at sea is level, and y0 is a constant. This density variation is called the law of atmospheres. Obtain this law assuming that the temperature of the atmosphere remains a constant (isothermal conditions). Also assume that the value of g remains constant.

Ans: The given volume of the balloon is, V = 1425 m3
Mass of the payload, m=400kg
And the acceleration due to gravity is, g=9.8m/s2
y0=8000m
The density of helium isρHe=0.18kgm−3
, and that of air at sea level is ρ0=1.25kgm−3
Let the density of the balloon be ρ and the height to which the balloon can rise be y.
The air density (ρ
) of decreases with increasing height (y ) as:
ρ/ρ0=e−y/y0
This relation is also called the law of atmospherics.
It can be inferred from the above law-equation that the rate of decrease of density with height is directly proportional to ρ
−dρdy∝ρ
⇒−dρdy=kρ
⇒−dρρ=kdy
Here, k is a proportionality constant.
We set the limits such that the height changes from 0 to y
, and the density varies from ρ0 to ρ
. ∫ρ0ρdρρ=∫0ykdy
Next, integrating the sides between these limits, we obtain:
[lnρ]ρρ0=−ky
⇒ρ/ρ0=e−ky
Comparing the above equation with the law of atmospherics, we get
⇒k=1y0
In conclusion, we have been able to derive the expression for the law of atmospherics.
(b) A large He balloon of volume 1425m3
is used to lift a payload of400 kg
. Assume that the balloon maintains a constant radius as it rises. How high does it rise? (Take y0=8000m and ρHe=0.18kgm−3 )
Ans: The generic expression for mass density is:
ρ=MV
In the current case, it becomes the total mass (including the payload and the helium) per unit volume of the balloon:
ρ=(Mpayload+MHe)V=m+VρHeV
⇒ρ=0.46kg/m3
Using the law of atmospherics, we can obtain the value of y
ρ/ρ0=e−y/y0
⇒lnρ/ρ0=−y/y0
⇒y=−8000×ln(0.46/1.25)=8000m=8km
Therefore, the balloon can rise to a height of 8 km.

---

Last Updated on: November 29, 2022