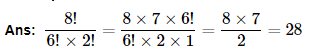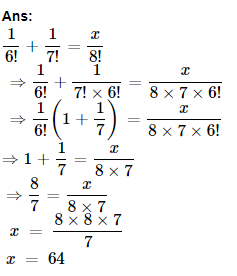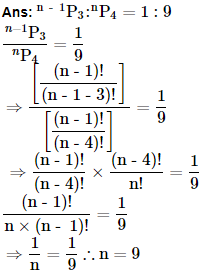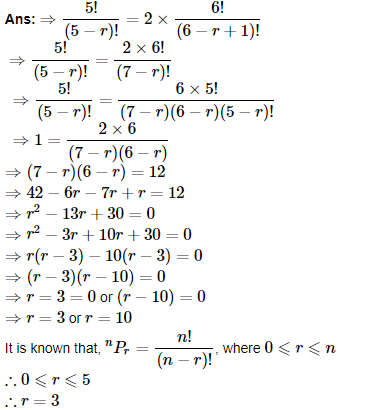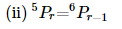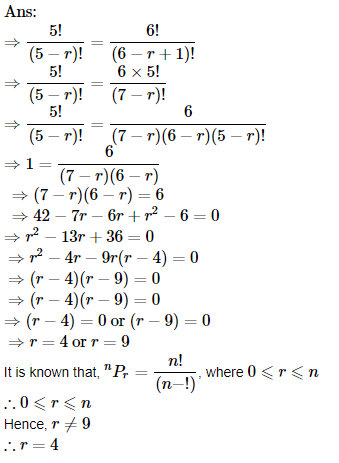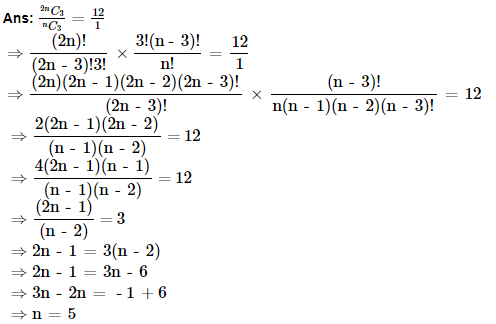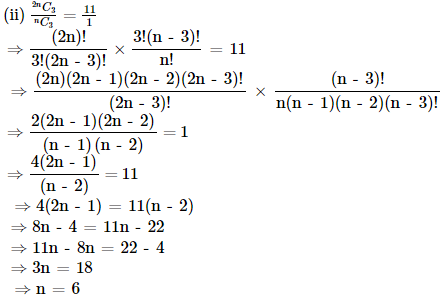Chapter 7 permutations and combinations Questions and Answers: NCERT Solutions for Class 11th Maths
Class 11 Maths Chapter 7: permutations and combinations - Questions and Answers of NCERT Book Solutions
Exercise 7.1
1. How many 3 -digit numbers can be formed from the digits 1, 2, 3, 4 and 5 assuming that
(i) Repetition of the digits is allowed?
(ii) Repetition of the digits is not allowed?
Ans: (i) There are as many ways of filling 3 empty places in succession by the given 5 digits. In the given case, repetition of digits is allowed. Thus, the units place can be filled in by any of the all 5 digits. Similarly, tens and hundreds digits can be filled by any of the all 5 digits. Thus, the number of ways in which 3-digit numbers can be formed from the given digits is 5×5×5=125.
(ii) In the given case, repetition of digits is not allowed. Thus, if units place is filled at first, then it can be filled by any of the given 5 digits. Thus, the number of ways is 5 . Similarly, the tens place can be filled by remaining 4 digits and the hundreds place can be filled by remaining three digits. Therefore, by multiplication principle, the number of ways = 5×4×3=60.
2. How many 3-digit even numbers cab be formed from the digits 1, 2, 3, 4, 5, 6 if the digits can be repeated?
Ans: There are ways of filling 3 empty places in succession by the given 6 digits. In the given case, the units place can be filled in by any of the all 6 digits. Similarly, tens and hundreds digits can be filled by any of the all 6 digits, as repetition is allowed. Thus, by multiplication principle, the required 3-digit even numbers is 3×6×6=108
3. How many 4-letter code can be formed using the first 10 letters of the English alphabet, if no letter can be repeated?
Ans: There are ways of filling 4 empty places in succession by the given 10 letters of the English alphabet, given that repetition is not allowed. The first place can be filled in 10 different ways any of the given 10 letters and second place can be filled in 9 different ways. Similarly third place can be filled in 8 different ways and the fourth in 7 different ways. Thus, by multiplication principle, the number of ways in which 4 empty places can be filled is 10×9×8×7=5040 Therefore, 5040 4-letter codes can be formed with the help of first 10 letters of English alphabet without repetition.
4. How many 5-digit telephone numbers can be constructed using the digits 0 to 9 if each number starts with 67 and no digit appears more than once?
Ans: Given: 5-digit telephone number starts with 67. Therefore, there are ways of filling the 3 empty spaces 6, 7, __, __, __ by digits 0-9 without repetition. Thus, units place can be filled in 8 different ways, tens place can be filled in 7 different ways and hundreds place can be filled in 6 different ways. Thus, by multiplication principle, number of ways in which 5-digit telephone number can be constructed is 8×7×6=336
5. A coin is tossed 3 times and the outcomes are recorded. How many possible outcomes are there?
Ans: When a coin is tossed once, there are 2 outcomes (head and tail) i.e., the number of ways of showing different face = 2 Thus, by multiplication principle, number of possible outcomes = 2×2×2=8
6. Given 5 flags of different colours, how many different signals can be generated if each signal requires the use of 2 flags, one below the other?
Ans: 1 signal = 2 flags. There are ways of filling 2 empty places in succession by the given 5 flags. The upper empty place can be filled in 5 different ways and the lower empty place can be filled in 4 different ways. Thus, by the multiplication principle, the ways in which different flags can be generated =5×4=20
Exercise 7.2
1. Evaluate (i) 8!
Ans: (i)8! = 1×2×3×4×5×6×7×8=40320
(ii) 4! – 3!
Ans: 4! = 1×2×3×4 = 24 3!=1×2×3 = 6 ∴4! - 3! = 24 - 6 = 18
2. Is 4! + 3! = 7!?
Ans: 3!=1×2×3 = 6 4! = 1×2×3×4 = 24 ∴3!+4!=6+24=30 7!=1×2×3×4×5×6×7=5040 ∴3!+4!≠7!
3. Compute
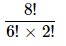
5.Evaluate

(i) n = 6, r = 2
Ans: (i)Whenn = 6,r = 2:
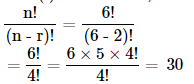
(ii) n = 9, r = 5
(ii)Whenn = 9,r = 5:
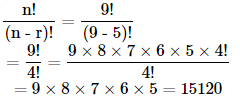
Exercise 7.3
1. How many 3-digit numbers can be formed by using the digits 1 to 9 if no digits is repeated?
Ans: Here, what matters is the order of digits.
Thus, there are permutations of 9 different digits taken 3 at a time.
Therefore, the number of 3-digit numbers =
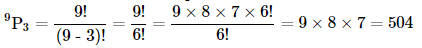
2. How many 4-digit numbers are there with no digit repeated?
Ans: The thousands place of the 4-digit number can be filled with any digit from 1 to 9 and 0 is not included. Thus, number of ways in which thousands place is filled is 9.
Also, the hundreds, tens and units place can be filled with any digit from 0 to 9. Since, te digits cannot be repeated and thousands place is already occupied by the digit. The hundreds, tens and units place can be filled by remaining 9 digits.
Thus, there are permutations of 9 different digits taken 3 at a time.
Number of 3-digit numbers =
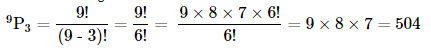
By, multiplication principle, number of 4-digit numbers is 9×504=4536
3. How many 3-digit even numbers can be made using the digits 1, 2, 3, 4, 6, 7, if no digit is repeated?
Ans: Using the numbers, 1, 2, 3, 4, 6 and 7, 3-digit numbers can be formed.
The units place can be filled by any of the digits 2, 4 or 6. Hence, there are 3 ways.
Since, it is given that, digits cannot be repeated, units place is already occupied, the hundreds and tens place can be occupied by remaining 5 digits.
Thus, number of ways of filling hundreds and tens place =
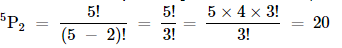
Therefore, by multiplication principle, number of 3-digit numbers = 3×20=60
4. Find the number of 4-digit numbers that can be formed using the digits 1, 2, 3, 4, 5 if no digit is repeated. How many of these will be even?
Ans: From the digits 1,2 ,3 ,4 and 5, 4-digit numbers can be formed.
There are permutations of 5 different things taken 4 at a time.
Thus, number of 4 digit numbers =
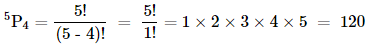
Out of 1, 2, 3, 4, 5, we know that even numbers end either by 2 or 4.
Thus, ways in which units place can be filled is 2.
Since, repetition is not allowed, units place is already occupied by a digit and remaining vacant places can be filled by remaining 4 digits.
Thus, number of ways in which remaining places can be filled =
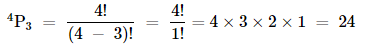
Therefore, by multiplication principle, number of even numbers = 24×2=48
5. From a committee of 8 persons, how many ways can we choose a chairman and a vice chairman assuming one person cannot hold more than one position.
Ans: In a committee of 8 persons, a chairman and vice chairman are selected in such away that one person can hold only one position.
Thus, ways of choosing a chairman and vice chairman is permutation of 8 objects taken 2 at a time
Therefore, number of ways
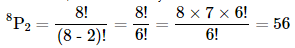
6. Find n if
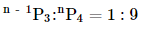
7. Find r if
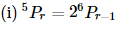
8. How many words, with or without meaning, can be formed using all the letters of the word EQUATION, using each letter exactly once?
Ans: The number of different letters in the given word is 8. Thus, the number of words than can be formed without repetition is number of permutations of 8 different objects taken 8 at a time = 8P8=8! Therefore, number of words formed = 8! = 40320.
9. How many words, with or without meaning can be made from the letters of the word MONDAY, assuming that no letter is repeated if,
(i) 4 letters are used at a time
(ii) all letters are used at a time
(iii) all letters are used but first letter is a vowel.
Ans: Number of different letters in the given word = 6
(i) Number of 4-letter words that can be formed from the letters of the given word without repetition is permutations of 6 different objects taken 4 at a time.
Therefore, Number of 4 letter words that can be formed
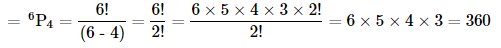
(ii) Words that can be formed using all the letters of the given word is permutation of 6 different objects taken 6 at a time
6P6=6!
Therefore, number of words that can be formed is
=6!=6×5×4×3×2×1=720
(iii) There are two different vowels in the word MONDAY which occupies the rightmost place of the words formed. Hence, there are 2 ways.
Since, it is without repetition and the rightmost place is occupied, the remaining five vacant places can be filled by 5 different letters. Hence, 5! Ways.
Therefore, number of words that can be formed = 5!×2=120×2=240
10. In how many of the distinct permutations of the letters in MISSISSIPPI do the four I’s not come together?
Ans: I appears 4 times, S appears 4 times, P appears 2 times and M appears one time in the given word
Thus, number of permutations of the given word
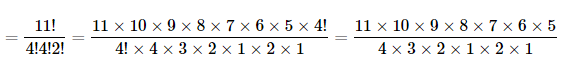
Since, there are 4 I’s in the given word, they can be treated as a single object. This single object with the remaining 7 objects will together be 8 objects.
These 8 objects in which 4 S’s and 2 P’s is arranged in 8!/4!2! = 840 ways
Thus, number of ways where I’s occur together = 840
Therefore, number of permutations where I’s do not occur together is =34650 – 840 = 33810
11. In how many ways can the letters of the word PERMUTATIONS can be arranged if the
(i) Words start with P and end with S.
(ii) Vowels are all together.
(iii) There are always 4 letters between P and S?
Ans: There are 2 T’s and other letters are repeated only once in the word PERMUTATION.
(i) Here, P and S are fixed at extreme ends (P at left and S at right end).
Hence, 10 letters are left.
Therefore, required number of permutations
10!/2!=1814400
(ii) Since, all the 5 vowels appear only once and they should always occur together, they can be treated as a single object.
This single object with the remaining 7 objects will be 8 objects.
Thus, 8 objects in which 2 T’s can be arranged together is
8!/2!ways
Also, the five different vowels can be arranged in 5! ways.
Thus, by multiplication principle, the number of arrangements
=8!/2!×5!=2419200
(iii) The letters can be arranged in such a way that there are 4 letters between P and S.
Thus, letters P and S are fixed. The remaining 10 letters in which 2 T’s is arranged in
10!2!ways.
Also, there are 4 letters between P and S = 2×7=14ways
Thus, by multiplication principle, the number of arrangements = 10!/2!×14=25401600
Exercise 7.4
1.If
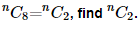
Ans:Since, we know that nCa=nCb⇒a=b or m=a+b
That is,
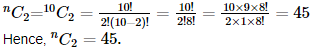
2. Determine n if
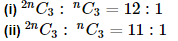
3. How many chords can be drawn through 21 points on a circle?
Ans: To draw one chord, 2 points are needed.
The number of combinations should be counted to find the number of chords to be drawn through the 21 points on the circle.
Thus, there are combinations of 21 points taken 2 at a time.
Therefore, number of chords is
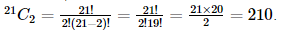
4. In how many ways can a team of 3 boys and 3 girls be selected from 5 boys and 4 girls.
Ans: Given: 3 boys and 3 girls are to be selected from 5 boys and 4 girls.
Out of 5 boys, 3 boys can be selected in 5C3 ways.
Out of 4 girls, 3 girls can be selected in 4C3 ways.
Therefore, by multiplication principle, number of ways in which a team of 3 boys and 3 girls can be selected =
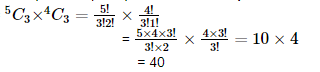
5. Find the number of ways of selecting 9 balls from 6 red balls, 5 white balls and 5 blue balls if each selection consists of 3 balls each colour.
Ans: Given: Total number of balls: 6 red balls, 5 white balls and 5 blue balls.
3 balls of each colour should be selected making a total of 9 balls.
Therefore,
Out of 6 red balls, 3 balls can be selected in 6C3 ways
Out of 5 white balls, 3 balls can be selected in 5C3 ways
Out of 5 blue balls, 3 balls can be selected in 5C3 ways
Therefore, by multiplication principle, number of ways of selecting 9 balls is =
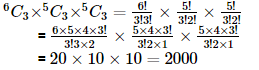
6.Determine the number of 5 card combinations out of a deck of 52 cards if there is exactly one ace in each combination.
Ans: There are 4 aces in a deck of 52 cards. A combination of 5 cards with one ace has to be made.
One ace is selected in 4C3 ways and the remaining 4 cards is selected from the 48 cards in 48C4 ways.
Therefore, by multiplication principle, Number of combinations is
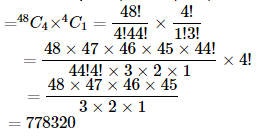
7. In how many ways can one select a cricket team of 11 from 17 players in which 5 players can bowl if each cricket team of 11 must include exactly 4 bowlers?
Ans: Given: There are 5 bowlers out of 17 players.
A cricket team of 11 is selected with exactly 4 bowlers.
Thus, 4 bowlers can be selected in 5C4 ways and out of remaining 12 players, 7 players are selected in 12C7 ways.
Thus, by multiplication principle, required number of ways of selecting cricket team =
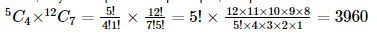
8. A bag contains 5 black and 6 red balls. Determine the number of ways in which 2 black and 3 red balls can be selected.
Ans: There are 5 black and 6 red balls in the bag.2 black balls can be selected out of 5 black balls in 5C2ways and 3 red balls can be selected out of 6 red balls in 6C3ways.
Thus, by multiplication principle, required number of ways of selecting 2 black and 3 red balls
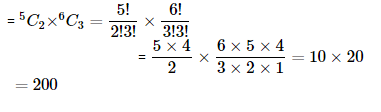
9.In how many ways can a student choose a programme of 5 courses if 9 courses are available and 2 specific courses are compulsory for every student?
Ans: Given: Out of 9 courses, 2 courses are compulsory.
Thus, out of the remaining 7 courses, every student has to choose 3 courses. This can be chosen in 7C3 ways.Thus, required number of ways of choosing the programme is:
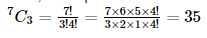
Last Updated on: December 05, 2025