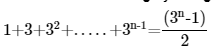- HOME
- |
- COLLEGES
- |
- TOP 10 COLLEGES
- |
- UNIVERSITIES
- |
- CAREER
- |
- HOW TO PREPARE
- |
- DATESHEET
Chapter 4 principle of mathematical induction Questions and Answers: NCERT Solutions for Class 11th Maths
Class 11 Maths Chapter 4: principle of mathematical induction - Questions and Answers of NCERT Book Solutions
Ans: Let us denote the given equality by P(n), i.e.,
Therefore, P(k+1) holds whenever P(k) holds.
Hence, the given equality is true for all natural numbers i.e., N by the principle of mathematical induction.
2. Prove the following by using the principle of mathematical induction for all n∈N:
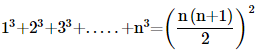
Ans: Let us denote the given equality by P(n), i.e.
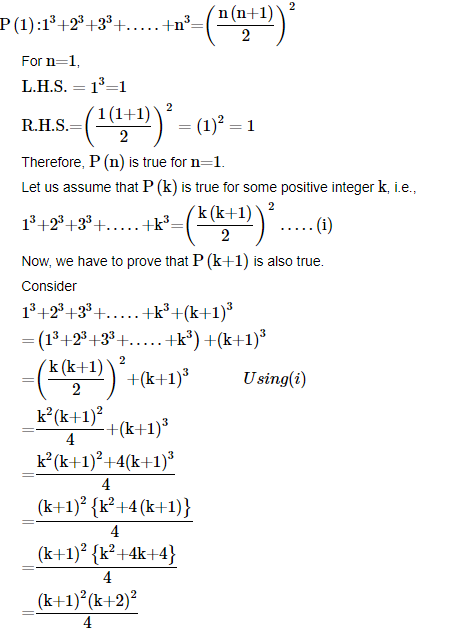
(k+1)2(k+1+1)2/4
((k+1)(k+1+1)/2)2
Therefore, P(k+1) holds whenever P(k) holds.
Hence, the given equality is true for all natural numbers i.e., N by the principle of mathematical induction.
3. Prove the following by using the principle of mathematical induction for all n∈N :
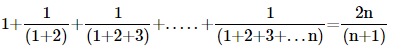
Ans: Let us denote the given equality by P(n), i.e.,
Therefore, P(k+1) holds whenever P(k) holds.
Hence, the given equality is true for all natural numbers i.e., N by the principle of mathematical induction.
4. Prove the following by using the principle of mathematical induction for all n∈N:
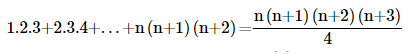
Ans: Let us denote the given equality by P(n), i.e.,
5. Prove the following by using the principle of mathematical induction for all n∈N:
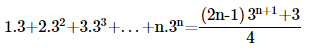
Ans: Let us denote the given equality by P(n), i.e.,
Therefore, P(k+1) holds whenever P(k) holds.
Hence, the given equality is true for all natural numbers i.e., N by the principle of mathematical induction.
6. Prove the following by using the principle of mathematical induction for all n∈N:
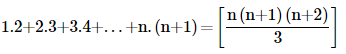
Ans: Let us denote the given equality by P(n), i.e.,
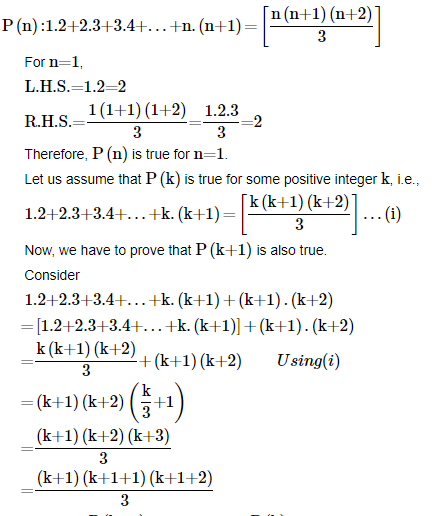Therefore, P(k+1) holds whenever P(k) holds.
Hence, the given equality is true for all natural numbers i.e., N by the principle of mathematical induction.
7. Prove the following by using the principle of mathematical induction for all n∈N:
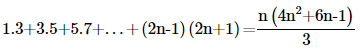
Ans: Let us denote the given equality by P(n), i.e.,
Therefore, P(k+1) holds whenever P(k) holds.
Hence, the given equality is true for all natural numbers i.e., N by the principle of mathematical induction.
8. Prove the following by using the principle of mathematical induction for all n∈N:
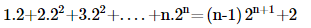
Ans: Let us denote the given equality by P(n), i.e.,
Therefore, P(k+1) holds whenever P(k) holds.
Hence, the given equality is true for all natural numbers i.e., N by the principle of mathematical induction
9. Prove the following by using the principle of mathematical induction for all n∈N:
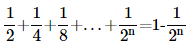
Ans: Let us denote the given equality by P(n), i.e.,
Hence, the given equality is true for all natural numbers i.e., N by the principle of mathematical induction.
10. Prove the following by using the principle of mathematical induction for all n∈N:
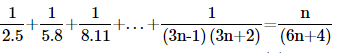
Ans: Let us denote the given equality by P(n), i.e.,
Therefore, P(k+1) holds whenever P(k) holds.
Hence, the given equality is true for all natural numbers i.e., N by the principle
of mathematical induction.
11. Prove the following by using the principle of mathematical induction for all n∈N:
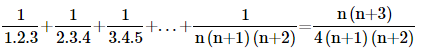
Ans: Let us denote the given equality by P(n), i.e.,
Therefore, P(k+1) holds whenever P(k) holds.
Hence, the given equality is true for all natural numbers i.e., N by the principle of mathematical induction.
12. Prove the following by using the principle of mathematical induction for all n∈N:
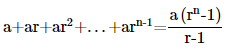
Ans: Let us denote the given equality by P(n), i.e.,
Therefore, P(k+1) holds whenever P(k) holds.
Hence, the given equality is true for all natural numbers i.e., N by the principle of mathematical induction.
13. Prove the following by using the principle of mathematical induction for all n∈N:
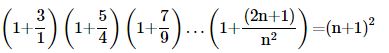
Ans: Let us denote the given equality by P(n), i.e.,
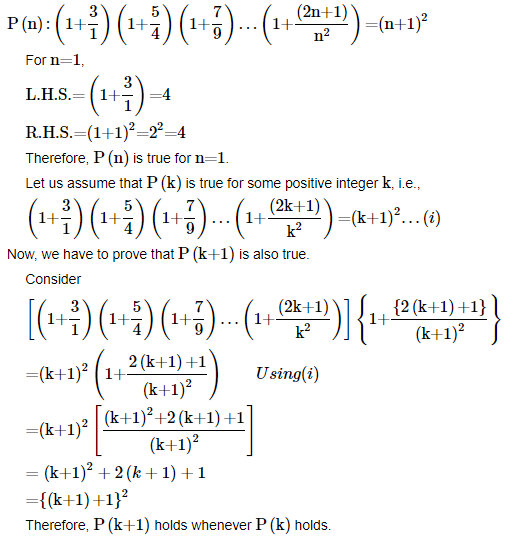Hence, the given equality is true for all natural numbers i.e., N by the principle of mathematical induction.
14. Prove the following by using the principle of mathematical induction for all n∈N:
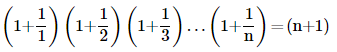
Ans: Let us denote the given equality by P(n), i.e.,
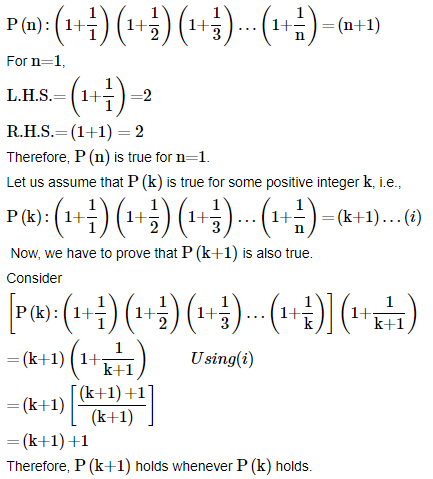Hence, the given equality is true for all natural numbers i.e., N by the principle of mathematical induction.
15. Prove the following by using the principle of mathematical induction for all n∈N:
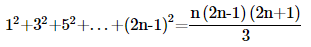
Ans: Let us denote the given equality by P(n), i.e.,
16. Prove the following by using the principle of mathematical induction for all n∈N:
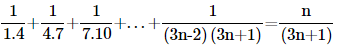
Ans: Let us denote the given equality by P(n), i.e.,
Hence, the given equality is true for all natural numbers i.e., N by the principle of mathematical induction.
17. Prove the following by using the principle of mathematical induction for all n∈N:
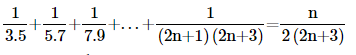
Ans: For n=1,
Therefore, P(k+1) holds whenever P(k) holds.
Hence, the given equality is true for all natural numbers i.e., N by the principle of mathematical induction.
18. Prove the following by using the principle of mathematical induction for all n∈N:
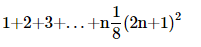
Ans: Let us denote the given equality by P(n), i.e.,
Hence, the given equality is true for all natural numbers i.e., N by the principle of mathematical induction.
19. Prove that following by using the principle of mathematical induction for all n∈N: n(n+1)(n+5)is a multiple of 3.
Ans: Let us denote the given statement by P(n), i.e.,
Hence, the given equality is true for all natural numbers i.e., N by the principle of mathematical induction.
20. Prove that following by using the principle of mathematical induction for all n∈N:
102n-1+1 is divisible by 11
Ans: Let us denote the given statement by P(n), i.e.,
Hence, the given equality is true for all natural numbers i.e., N by the principle of mathematical induction.
21. Prove that following by using the principle of mathematical induction for all n∈N:
x2n-y2n is divisible by x+y.
Ans: Let us denote the given statement by P(n), i.e.,
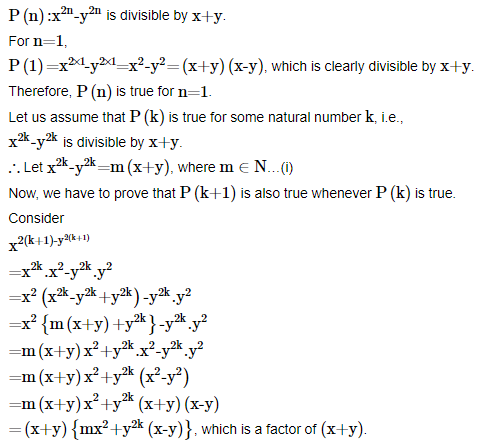
Therefore, P(k+1) holds whenever P(k) holds.
Hence, the given equality is true for all natural numbers i.e., N by the principle of mathematical induction.
22. Prove that following by using the principle of mathematical induction for all n∈N:
32n+2-8n-9 is divisible by 8.
Ans: Let us denote the given statement by P(n), i.e.,
Hence, the given equality is true for all natural numbers i.e., N by the principle of mathematical induction.
23. Prove that following by using the principle of mathematical induction for all n∈N:
41n-14n is a multiple of 27.
Ans: Let us denote the given statement by P(n), i.e.,
Hence, the given equality is true for all natural numbers i.e., N by the principle of mathematical induction.
24. Prove that following by using the principle of mathematical induction for all n∈N:
(2n+7)(n+3)2
Ans: Let us denote the given statement by P(n), i.e.,
Hence, the given equality is true for all natural numbers i.e., N by the principle of mathematical induction.
Last Updated on: Mar 26, 2024
