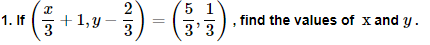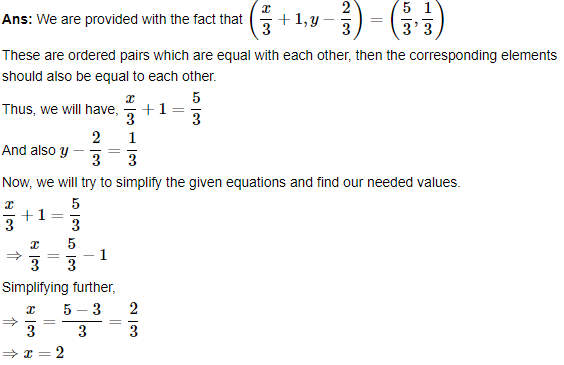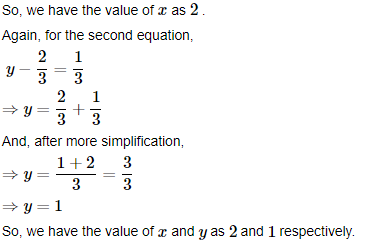Chapter 2 Relation and Functions Questions and Answers: NCERT Solutions for Class 11th Maths
Class 11 Maths Chapter 2: Relation and Functions - Questions and Answers of NCERT Book Solutions
Exercise 2.1
2. If the set A has 3 elements and the set B={3,4,5} , then find the number of elements in (A×B) ?
Ans: We are provided with the fact that the set A has 3 elements and the set B is given as {3,4,5} . So, the number of elements in set B is 3 . Thus, the number of elements in (A×B) will be, = Number of elements in A× Number of elements in B =3×3=9 So, the number of elements in (A×B) is 9
3. If G={7,8} and H={5,4,2} , find G×H and H×G
Ans: We have the sets G={7,8} and H={5,4,2} . The Cartesian product of two non-empty sets A and B is defined as A×B={(a,b):a∈Aandb∈B} So, the value of G×H will be, G×H={(7,5),(7,4),(7,2),(8,5),(8,4),(8,2)} And similarly the value of H×G will be, H×G={(5,7),(5,8),(4,7),(4,8),(2,7),(2,8)}
4. State whether each of the following statement are true or false. If the statement is false, rewrite the given statement correctly.
(i) If P={m,n} and Q={n,m} , then P×Q={(m,n),(n,m)} .
Ans: The statement is False. We have the value as, P={m,n} and Q={n,m}. Thus, P×Q={(m,m),(m,n),(n,m),(n,n)}
(ii) If A and B are non-empty sets, then A×B is a non-empty set of ordered pairs (x,y) such that x∈A and y∈B.
Ans: The statement is True.
(iii) If A={1,2},B={3,4} , then A×{B∩∅}=∅ .
Ans: The statement is True. We know, B∩∅=∅ Thus, we have, A×{B∩∅}=A×∅=∅.
5. If A={−1,1} , find A×A×A .
Ans: For any non-empty set A , the set A×A×A is defined by, A×A×A={(p,q,r):p,q,r∈A} Now, we are provided with the fact that, A={−1,1} Thus, A×A×A={(−1,−1,−1),(−1,−1,1),(−1,1,−1),(−1,,1,1),(1,−1,−1),(1,−1,1),(1,1,−1),(1,1,1)}
6. If A×B={(a,x),(a,y),(b,,x),(b,y)} . Find A and B .
Ans: We are provided with the fact that A×B={(a,x),(a,y),(b,x),(b,y)} On the other hand, the Cartesian product of two non-empty sets A and B is defined as A×B={(a,b):a∈Aandb∈B} As we can see, A is the set of all the first elements and B is the set of all the second elements. So, we will have, A={a,b} and B={x,y} .
7. Let A={1,2},B={1,2,3,4},C={5,6} and D={5,6,7,8} . Verify that
(i) A×(B∩C)=(A×B)∩(A×C)
Ans: We are provided with 3 sets and we have to prove A×(B∩C)=(A×B)∩(A×C) To start with, we will have, B∩C=∅ , as there are no elements in common between these sets. Thus, we have, A×(B∩C)=A×∅=∅ For the right hand side, we have, A×B={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4)} And similarly, A×C={(1,5),(1,6),(2,5),(2,6)} Again, we can see there are no elements in common between these sets. So, we have, (A×B)∩(A×C)=∅ So, we get, L.H.S = R.H.S.
(ii) A×C is a subset of B×D
Ans: Again, we are to verify, A×C is a subset of B×D So, we have, A×C={(1,5),(1,6),(2,5),(2,6)} And similarly, B×D={(1,5),(1,6),(1,7),(1,8),(2,5),(2,6),(2,7),(2,8),(3,5),(3,6),(3,7),(3,8),(4,5),(4,6),(4,7),(4,8)} We can easily see, every element of A×C is an element of B×D . So, A×C is a subset of B×D .
8. Let A={1,2} and B={3,4} . Write A×B . How many subsets will A×B have? List them.
Ans: We are provided with the fact that A={1,2} and B={3,4} Thus, we have, A×B={(1,3),(1,4),(2,3),(2,4)} So, the set A×B has 4 elements. Now, this is also known to us that, if a set A has n elements, then the number of subsets of Ais 2n . We can thus conclude that, A×Bwill have 24=16 subsets. Now, noting down the subsets of A×B we get, ∅,{(1,3)},{(1,4)},{(2,3)},{(2,4)},{(1,3),(1,4)}, {(1,3),(2,3)},{(1,3),(2,4)}, {(1,4),(2,3)},{(1,4),(2,4)},{(2,3),(2,4)}, {(1,3),(1,4),(2,3)},{(1,3),(1,4),(2,4)}, {(1,3),(2,3),(2,4)},{(1,4),(2,3),(2,4)}, {(1,3),(1,4),(2,3),(2,4)}
9. Let A and B be two sets such that n(A)=3 and n(B)=2 . If (x,1),(y,2),(z,1) are in A×B , find A and B , where x,y and z are distinct elements.
Ans: We are provided with the fact that n(A)=3 and n(B)=2 ; and(x,1),(y,2),(z,1) are in A×B . We also know that, A is the set of all the first elements and B is the set of all the second elements. So, we can conclude, A having elements x,y,z and B having elements 1,2 . Thus, we get, n(A)=3,n(B)=2. So, A={x,y,z},B={1,2}
10. The Cartesian product A×A has 9 elements among which are found (−1,0) and (0,1) . Find the set A and the remaining elements of A×A .
Ans: We are provided with, n(A×A)=9 . We also know that, if n(A)=a,n(B)=b , then n(A×B)=ab As it is given that, n(A×A)=9 It can be written as, n(A)×n(A)=9 ⇒n(A)=3 And it is also given that (−1,0),(0,1) are the two elements of A×A . Again, the fact is also known that, A×A={(a,a):a∈A} . And also −1,0,1 are the elements of A . Also, n(A)=3 , implies A={−1,0,1} . So, (−1,−1),(−1,1),(0,−1),(0,0),(1,−1),(1,0),(1,1) are the remaining elements of A×A .
Exercise 2.2
1. Let A={1,2,3,......,14} . Define a relation R from A to A by R={(x,y):3x−y=0} , where x,y∈A . Write down its domain, codomain and range.
Ans: We are given with the relation R from A to A as, R={(x,y):3x−y=0} where x,y∈A . So, we can write R as, R={(1,3),(2,6),(3,9),(4,12)} . Thus, the domain of R is, {1,2,3,4} . And similarly, the range of R is, {3,6,9,12} . And also, the codomain of R is, A={1,2,3,......,14} .
2. Define a relation R on the set N of natural numbers by R=(x,y) : y=x+5x is a natural number less than 4; x,y in N . Depict this relationship using roster form. Write down the domain and the range.
Ans: We are given with the fact that, R=(x,y): y=x+5,x is a natural number less than 4; x,y in N. We have the value of x as 1,2,3 are it must be less than 4. So, the relation R will look like, R={(1,6),(2,7),(3,8)} The domain of R will be, ={1,2,3} And similarly, the range of R will be, ={6,7,8} .
3. A={1,2,3,5} and B={4,6,9} . Define a relation R from A to B by R=(x,y):the difference between x and y is odd; x in A,y in B . Write R in roster form.
Ans: We are provided with the fact that A={1,2,3,5} and B={4,6,9} . We are also given that, R=(x,y):the difference between x and y is odd; x in A,y in B Simply, writing down according to the given condition, R={(1,4),(1,6),(2,9),(3,4),(3,6),(5,4),(5,6)}
4. The given figure shows a relationship between the sets P and Q .
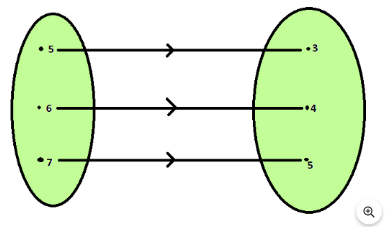
Write this relation
(i) In set-builder form
Ans: From the given figure in the problem, we have, P={5,6,7},Q={3,4,5} Now, writing the relation in the set-builder form, (i)R={(x,y):y=x−2;x∈P} And in another form, R={(x,y):y=x−2;x∈5,6,7}
(ii) In roster form
What is its domain and range?
Ans: From the given figure in the problem, we have, P={5,6,7},Q={3,4,5} And again, in roster form, (ii)R={(5,3),(6,4),(7,5)} Where the domain of R is{5,6,7} and range of R is{3,4,5} .
5. Let A={ 1,2,3,4,6 } . Let R be the relation on A defined by (a,b):a,b in A,b is exactly divisible by a .
(i) Write R in roster form.
Ans: We are provided with the fact that,$A=\{1,2,3,4,6\},R=(a,b):a,b in A,b is exactly divisible by a Using the conditions given in the problem, we get, R={(1,1),(1,2),(1,3),(1,4),(1,6),(2,2), (2,4),(2,6),(3,3),(3,6),(4,4),(6,6)} And this is the roster form of the relation.
(ii) Find the domain of R
Ans: We can clearly see, the domain of R is, {1,2,3,4,6}
(iii) Find the range of R.
Ans: And similarly, the range of R is, {1,2,3,4,6}
6. Determine the domain and range of the relation R defined by R={(x,x+5):x∈{0,1,2,3,4,5}}
Ans: We are provided with the fact, R={(x,x+5):x∈{0,1,2,3,4,5}} Using the condition given, We can clearly write that, R={(0,5),(1,6),(2,7),(3,8),(4,9),(5,10)} And this is our needed relation. Now, it can be clearly observed, that the domain of R is, {(x:x∈(0,1,2,3,4,5)}. And similarly, the range of R is, {(y:y∈(5,6,7,8,9,10)}.
7. Write the relationR=(x,x3): x is a prime number less than 10 in roster form.
Ans: We are provided with the fact that, R={(x,x3):xisaprimenumberlessthan10} . We know, the prime numbers less than 10 are 2,3,5,7 . Thus, the relation can be written as, R={(2,8),(3,27),(5,125),(7,343)}
8. Let A={x,y,z} and B={1,2} . Find the number of relations from A to B .
Ans: The facts provided to us are, A={x,y,z} and B={1,2} . Now, we will try to find out the Cartesian product of these to sets, A×B={(x,1),(x,2),(y,1),(y,2),(z,1),(z,2)} Thus, we see, the number of elements in A×B is 6 . So, the number of subsets, 26 . Then, the number of relations from A to B is 26 .
9. Let R be the relation on Z defined by R={(a,b):a,b∈Z,a−bisaninteger} . Find the domain and range of R .
Ans: The relation is given as, R={(a,b):a,b∈Z,a−bisaninteger} . And, we know the fact that, the difference of two given integers in always an integer. Thus, it can be concluded that, Domain of R is Z and similarly, the range of R is also Z .
Exercise 2.3
1. Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.
(i) {(2,1),(5,1),(8,1),(11,1),(14,1),(17,1)}
Ans: We have the given relation as, {(2,1),(5,1),(8,1),(11,1),(14,1),(17,1)} . Thus, we can see, the domain of the relation consists of {2,5,8,11,14,17} and range is {1} . And we also have, every element of the domain is having their unique images, then it is a function.
(ii) {(2,1),(4,2),(6,3),(8,4),(10,5),(12,6),(14,7)}
Ans: We have our given relation, {(2,1),(4,2),(6,3),(8,4),(10,5),(12,6),(14,7)}. Thus, we have our domain as, {2,4,6,8,10,12,14} and range as, {1,2,3,4,5,6,7} . Every element of the domain is having their unique images, so this is a function.
(iii) {(1,3),(1,5),(2,5)}
Ans: Our given relation is, {(1,3),(1,5),(2,5)}. From the domain of the relation the element 1 is having two different images 3,5 . So,every element of the domain is not having their unique images. So, this is not a function.
2. Find the domain and range of the following real function:
(i)f(x)=−|x|
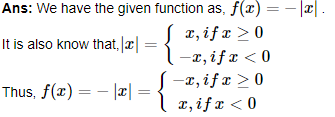
As the function is a real function, the domain of the function is R .
And again, we can see that the function is giving values of all real numbers except positive ones.
So, the range of the function is, (−∞,0] .
(ii)f(x)=√9−x2−−−−−
3. A function is defined by f(x)=2x−5
(i) f(0)
Ans: We have the given function as, f(x)=2x−5 So, the value of, f(0)=2×0−5=−5
(ii) f(7)
Ans: We have the given function as, f(x)=2x−5 So, the value of, f(7)=2×7−5=14−5=9
(iii) f(−3)
Ans: We have the given function as, f(x)=2x−5 So, the value of, f(−3)=2×(−3)−5=−6−5=−11
4. The function ′t′ which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by t(C)=9C5+32 . Find
(i) t(0)
Ans: We have our given function as, t(C)=9C5+32 . Thus, to find our needed values of the function we just have to put the values in the given function and simplify it. So, we get now, t(0)=9×05+32=32
(ii) t(28)
(iii) t(−10)
(iv) The value of C, when t(C)=212 .
5. Find the range of each of the following functions:
(i) f(x)=2−3x,x∈R,x>0 .
(ii) f(x)=x2+2,xisarealnumber.
(iii) f(x)=x,x is a real number .
Ans: We have our given function as, f(x)=x,xisarealnumber . Now, we can clearly have, that the range of the function is the set of all the numbers. So, the range of the function will be, R .
Last Updated on: December 05, 2025