Chapter 6 linear inequalities equations Questions and Answers: NCERT Solutions for Class 11th Maths
Class 11 Maths Chapter 6: linear inequalities equations - Questions and Answers of NCERT Book Solutions
Exercise 6.1
1. Solve 24x<100, when
Ans: The given inequality is24x<100.
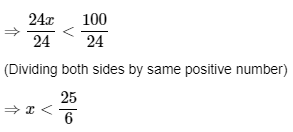
(i) x is a natural number-
1,2,3 and 4 are the only natural numbers that are smaller than 25\ 6 . When x is a natural number, the above inequality's solutions are 1,2,3 and 4. As a result, the solution set in this example is( 1, 2 ,3 ,4 ).
(ii) x is an integer-
When x is an integer.
Suppose the given x is an integer then by the integer definition we have (−∞,∞) which means there is no end at positive and negative values and then we have {…,−3,−2,−1,0,1,2,3,….}}
Thus, the value of x as integers is {…,−3,−2,−1,0,1,2,3,4} after four which is a greater value.
2. Solve−12x>30, when
Ans: The given inequality is−12x>30.
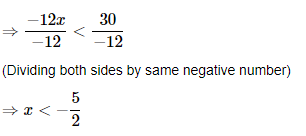
(i) x is a natural number-
There isn't a natural number that isn't less than (−5/2). As a result there is no solution to the given inequality when it is a natural number.
(ii) x is an integer-
The integers less than (−5/2) are…−5,−4,−3. As a result, when an integer is an integer, the above inequality's solutions are …..−5,−4,−3 As a result, the solution set in this situation is {.......,−5,−4,−3}.
3. Solve 5x−3<7, when
Ans: The given inequality is 5x−3<7.
⇒5x−3+3<7+3
⇒5x<10
⇒5x5<105
⇒x<2
(i) x is an integer-
The integers less than 2 are ..., −4,−3,−2,−1,0,1. As a result, the solutions to the above inequality are when is an integer…,−4,−3,−2,−1,0,1. As a result, the solution set in this example is {⋯,−4,−3,−2,−1,0,1}.
(ii) x is a real number-
When x is a real number, the inequality's solutions are x<2, that is, all real values x less than 2. As a result, the given inequality's solution set is x∈(−∞,2).
4. Solve 3x+8>2, when
Ans: The given inequality is 3x+8>2 3x+8>2
⇒3x+8−8>2−8
⇒3x>−6
⇒3x3>−63
⇒x>−2
(i) x is an integer-
The integers higher than −2 are −1,0,1,2,… Hence, when is an integer, the solutions of the above inequality are −1,0,1,2,… Hence, the solution set in this case is {−1,0,1,2,…} -
(ii) x is a real number-
When x is a real number, the above inequality's solutions are all real numbers that are bigger than -2. As a result, the solution set in this situation is (−2,∞).
5. Solve the given inequality for real x:4x+3<5x+7
Ans: 4x+3<5x+7
⇒4x+3−7<5x+7−7
⇒4x−4<5x
⇒4x−4−4x<5x−4x
⇒-4< x
As a result, all real numbers x bigger than -4 are solutions to the given inequality. As a result, the given inequality's solution set is (−4,∞).
6. Solve the given inequality for real x:3x−7>5x−1
Ans: 3x−7>5x−1
⇒3x−7+7>5x−1+7
⇒3x>5x+6
⇒3x−5x>5x+6−5x
⇒−2x>6
⇒−2x−2<6−2
⇒x<−3
As a result, all real numbers x less than -3 are solutions to the given inequality. As a result, the given inequality's solution set is (−∞,−3)
7. Solve the given inequality for real x:3(x−1)⩽2(x−3)
Ans: 3(x−1)⩽2(x−3) ⇒3x−3⩽2x−6 ⇒3x−3+3⩽2x−6+3 ⇒3x⩽2x−3 ⇒3x−2x⩽2x−3−2x ⇒x⩽−3 As a result, any real numbers x less than or equal -3 to are solutions to the specified inequality. As a result, the given inequality's solution set is (−∞,−3].
8. Solve the given inequality for real x:3(2−x)⩾2(1−x)
Ans: 3(2−x)⩾2(1−x) ⇒6−3x⩾2−2x ⇒6−3x+2x⩾2−2x+2x ⇒6−x⩾2 ⇒6−x−6⩾2−6 ⇒−x⩾−4 ⇒x⩽4 As a result, the solutions to the following inequality are all real values x higher than or equal to 4. As a result, the given inequality's solution set is (−∞,4].
9. Solve the given inequality for real.
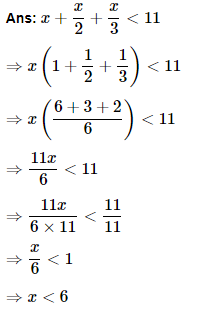
As a result, all real numbers x less than 6 are solutions to the specified inequality. As a result, the given inequality's solution set is (−∞,6).
10. Solve the given inequality for real
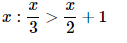
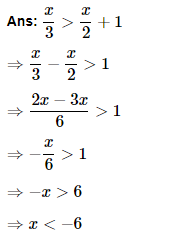
As a result, all real numbers less than equal the specified inequality's solution. As a result, the solution set for the given inequality is (−∞,−6).
11. Solve the given inequality for real
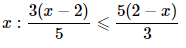
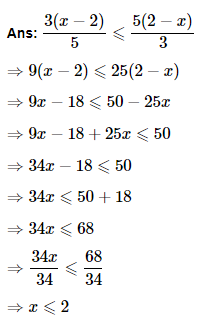
As a result, any real numbers x less than or equal to 2 are solutions of the above inequality, and hence the solution set of the given inequality is (−∞,2].
12. Solve the given inequality for real
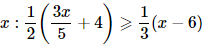
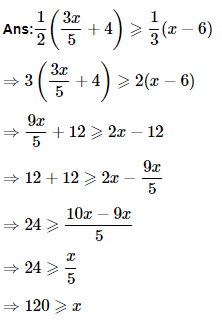
As a result, the solutions of the following inequality are all real values x less than or equal to 120. As a result, the given inequality's solution set is (−∞,120].
13. Solve the given inequality for real x:2(2x+3)−10<6(x−2)
Ans: 2(2x+3)−10<6(x−2)
⇒4x+6−10<6x−12
⇒4x−4<6x−12
⇒−4+12<6x−4x
⇒8<2x
⇒4 < x
As a result, any real numbers x bigger than 4 are solutions to the specified inequality. As a result, the given inequality's solution set is (4,−∞).
14. Solve the given inequality for real x:37−(3x+5)⩾9x−8(x−3)
Ans: 37−(3x+5)⩾9x−8(x−3) ⇒37−3x−5⩾9x−8x+24 ⇒32−3x⩾x+24 ⇒32−24⩾x+3x ⇒8⩾4x ⇒2⩾x As a result, the solutions of the following inequality are all real values x less than or equal to 2. As a result, the given inequality's solution set is (−∞,2].
15. Solve the given inequality for real
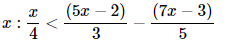
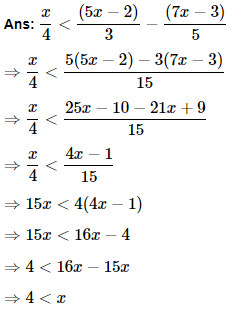
As a result, any real numbers x bigger than 4 are solutions to the specified inequality. As a result, the given inequality's solution set is (4,∞).
16. Solve the given inequality for real
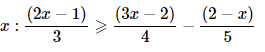
As a result, the solutions of the following inequality are all real values x less than or equal to 2. As a result, the given inequality's solution set is (−∞,2].
21. Ravi obtained 70 and 75 marks in first two-unit test. Find the minimum marks he should get in the third test to have an average of at least 60 marks.
Ans: Let x represent Ravi's score on the third unit test. Because the student must have a grade point average of at least 60,
70+75+x/3< 60
⇒145+x⩾180
⇒x⩾180−145
⇒x⩾35
As a result, the student must score at least 35 points to achieve a 60-point average
22. To receive Grade ' A∗ in a course, one must obtain an average of 90marks or more in five examinations (each of 100 marks). If Sunita"s marks in first four examinations are 87,92,94 and 95, find minimum marks that Sunita must obtain in fifth examination to get grade ' A " in the course.
Ans: Let x represent Sunita's grade in the fifth examination. She must receive an average of 90 or above in five examinations in order to receive a grade of in the course,
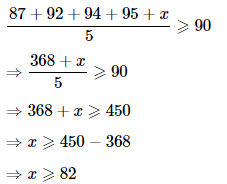
Sunita must therefore achieve a score of at least 82 in the fifth examination.
23. Find all pairs of consecutive odd positive integers both of which are smaller than 10 such that their sum is more than 11 .
Ans: Let x be the lesser of the two odd positive integers that follow. Then there's x + 2 as the other integer. Because both integers are less than 10 , x+2<10 ⇒x<10−2 ⇒x<8….(t) Furthermore, the sum of the two integers exceeds 11.∴x+(x+2)>11 ⇒2x+2>11 ⇒2x>11−2 ⇒2x>9 ⇒x>92 ⇒x>4.5 We get I and (ii) from I and (ii). Because x is an odd number, the values 5 and 7 can be used. As a result, the required pairs are (5,7) and (7,9).
24. Find all pairs of consecutive even positive integers, both of which are larger than 5 such that their sum is less than 23 .
Ans: Let be the smaller of the two even positive integers that follow. The other integer is x + 2
because both integers are greater than 5, x>5……(1)
Also, the sum of the two integers is less than 23 x+(x+2)<23
⇒2x+2<23
⇒2x<23−2
⇒2x<21
⇒x<212
⇒x<10.5……(2)
From (1) and (2), we obtain 5 < x <10.5
Because x is an even number, it can have any of the following values: 6,8, or 10.
As a result, the required pairs are (6,8),(8,10) and (10,12).
25. The longest side of a triangle is 3 times the shortest side and the third side is 2cm shorter than the longest side. If the perimeter of the triangle is at least 61cm, find the minimum length of the shortest side.
Ans: Determine the length of the triangle's shortest side xcm. Then, length of the longest side =3xcm Length of the third side (3x−2)cm Since the perimeter of the triangle is at least 61cm, xcm+3xcm+(3x−2)cm⩾61cm ⇒7x−2⩾61 ⇒7x⩾61+2 ⇒7x⩾63 ⇒7x7⩾637 ⇒x⩾9 As a result, the shortest side's minimal length is 9cm.
26. A man wants to cut three lengths from a single piece of board of length 91cm. The second length is to be 3cm longer than the shortest and the third length is to be twice as bang as the shortest. What are the possible lengths of the shortest board if the third piece is to be at least 5cm longer than the second? Hint:It$x$isthelengthoftheshortestboard,then$x,(x+3)$and$2x$arethelengthsofthesecondandthirdpiece,respectively.Thus,$x=(x+3)+2x⩽91$and$2x⩾(x+3)+5
Ans: The shortest piece's length should be xcm. Then, length of the second piece and the third piece are (x+3)cm and 2xcm respectively. Since the three lengths are to be cut from a single piece of board of length 91cm, xcm+(x+3)cm+2xcm⩽91cm ⇒4x+3⩽91 ⇒4x⩽91−3 ⇒4x⩽88 ⇒4x4⩽884 ⇒x⩽22….(1) In addition, the third component is at least 5 cm as long as the second. ∴2x⩾(x+3)+5 ⇒2x⩾x+8 ⇒x⩾8 From (1) and (2), we obtain 8⩽x⩽22 As a result, the smallest board's potential length is larger than or equal to but less than or equal to 22cm.
Exercise 6.2
1. Solve the given inequality graphically in two-dimensional plane :x+y<5
Ans: The visual representation of thex+y=5 In the diagram below, is shown as a dotted line. This line separates the two groups. xy− Split the plane into two half-planes. and II Choose a point (not on the line) that lies in one of the half planes to see if it meets the stated inequality or not.

The point is chosen as (0,0). It is observed that. 0+0<5 or 0<5, Because half plane II is not the solution zone of the given inequality, it is true. Furthermore, any point on the line clearly does not satisfy the provided stringent inequality. As a result, the shaded half plane I, excluding the points on the line, is the solution region of the given inequality.
This can be expressed in the following way:
2. Solve the given inequality graphically in two-dimensional plane: 2x+y⩾6
Ans: The graphical representation of 2x+y=6 is given in the figure below. The xy-plane is divided into two half planes, I and II, by this line. To determine whether a point (not on the line) in one of the half planes fulfils the given inequality, choose a point (not on the line) that lies in one of the half planes. The point is chosen as (0,0).

It is observed that, 2(0)+0⩾6 or 0⩾6, Because half plane I is not the solution zone of the given inequality, it is false. Furthermore, any point on the line must satisfy the stated inequality. As a result, the shaded half plane II, which includes the points on the line, is the solution region of the given inequality. As an example, consider the following.
3. Solve the given inequality graphically in two-dimensional plane: 3x+4y⩽12
Ans: 3x+4y⩽12
The graphical representation of 3x+4y=12is depicted in the diagram below. The xy-plane is divided into two half planes, I and II, by this line. To determine whether a point (not on the line) in one of the half planes fulfils the given inequality, choose a point (not on the line) that lies in one of the half planes.point is chosen as (0,0). As a result, the shaded half plane I, which includes the points on the line, is the solution region of the given inequality. The following is an example of how this could be represented.

4. Solve the given inequality graphically in two-dimensional plane: y+8⩾2x
Ans : The graphical representation of y+8=2x is depicted in the diagram below.
The xy-plane is divided into two half planes by this line. To determine whether a point (not on the line) in one of the half planes fulfils the given inequality, choose a point (not on the line) that lies in one of the half planes. The point is chosen as
(0,0).

It is observed that, 0+8⩾2(0) or 8⩾0, As a result, the solution zone of the given inequality is not the lower half plane. Furthermore, any point on the line must satisfy the stated inequality. As a result, the half plane containing the point ( 0,0 ) and the line is the solution region of the stated inequality. The dark zone represents the solution region as follows.
5. Solve the given inequality graphically in two-dimensional plane: x−y⩽2
Ans: The graphical representation of x−y=2 is depicted in the diagram below. The xy-plane is divided into two half planes by this line. To determine whether a point (not on the line) in one of the half planes fulfils the given inequality, choose a point (not on the line) that lies in one of the half planes.

The point is chosen as (0,0). It is observed that, 0−0⩽2 or 0⩽2, As a result, the solution zone of the given inequality is not the lower half plane. Furthermore, any point on the line clearly satisfies the specified inequality. As a result, the half plane containing the point ( 0,0 ) and the line is the solution region of the stated inequality. The dark zone represents the solution region as follows.
6. Solve the given inequality graphically in two-dimensional plane: 2x−3y>6
Ans: The graphical representation of 2x−3y=6 is given as dotted line in the figure below. This line divides the xy-plane in two half planes. Seloct a point (not on the line), which lies in one of the half planes, to determine whether the point satisfies the given inequality or not. We select the point as (0,0).

It is observed that. As a result, the solution zone of the given inequality is not the upper half plane. Furthermore, any point on the line clearly does not satisfy the specified inequality. As a result, the half plane that does not contain the point ( 0,0 ) including the line is the solution region of the stated inequality. The dark zone represents the solution region as follows.
2(0)−3(0)>6 or 0>6,
7. Solve the given inequality graphically in two-dimensional plane: −3x+2y⩾−6
Ans: The graphical representation of −3x+2y=−6is depicted in the diagram below. The xy-plane is divided into two half planes by this line. To determine whether a point (not on the line) in one of the half planes fulfils the given inequality, choose a point (not on the line) that lies in one of the half planes.

The point is chosen as (0,0). It is observed that, −3(0)+2(0)⩾−6 or 0⩾−6, As a result, the solution zone of the given inequality is not the lower half plane. Furthermore, any point on the line must satisfy the stated inequality. As a result, the half plane containing the point ( 0, 0 ) including the line is the solation zone of the stated inequality. The dark zone represents the solution region as follows.
8. Solve the given inequality graphically in two-dimensional plane: 3y−5x<30
Ans: The graphical representation of 3y−5x=30 In the diagram below, is shown as a dotted line. The xy-plane is divided into two half planes by this line. To determine whether a point (not on the line) in one of the half planes fulfils the given inequality, choose a point (not on the line) that lies in one of the half planes.

The point is chosen as (0,0). It is observed that, 3(0)−5(0)<30 or 0>30, As a result, the upper half plane does not contain the solution region for the stated inequality. Furthermore, any point on the line clearly does not satisfy the specified inequality.
As a result, the half plane containing the point ( 0,0 ) excluding the line is the solution zone of the stated inequality. The dark zone represents the solution region as follows.
9. Solve the given inequality graphically in two-dimensional plane: y<−2
Ans: The graphical representation of y=−2 The figure below shows this as a dotted line. The xy-plane is split into two halves by this line. To determine whether or not a point (not on the line) in one of the half planes fulfils the specified inequality, choose a point (not on the line) that is in one of the half planes.

The point is chosen as follows: (0,0). It is observed that, 0<−2, which is false.
Furthermore, any point on the line clearly does not satisfy the specified inequality. As a result, the solution of the above inequality is determined by every point below the line, y = -2 (excluding all points on the line). The darker zone represents the solution region as follows:
10. Solve the given inequality graphically in two-dimensional plane: x>−3
Ans: The graphical representation of x=−3 In the diagram below, is shown as a dotted line. The xy-plane is divided into two half planes by this line. To determine whether a point (not on the line) in one of the half planes fulfils the given inequality, choose a point (not on the line) that lies in one of the half planes.

The point is chosen as (0,0). It is observed that, 0<−3,This is also true, as any point on the line clearly does not satisfy the provided inequality. As a result, the solution of the above inequality is determined by every point on the right side of the line, x = - 3 (excluding all points on the line). The darker zone represents the solution region as follows:
Exercise 6.3
1. Solve the following system of inequalities graphically: x⩾3,y⩾2.
Ans: x⩾3…(1) y⩾2……(2) The graph of the lines, x=3 and y=2, are drawn in the figure below. Inequality (1) represents the region on the right hand side of the line, x=3 (including the line x=3 ). Inequality ( 2 ) represents the region above the line, y=2 (including the line y=2 ). Hence, the solution of the given system of linear inequalities is represented by the common shaded region including the points on the respective lines as follows.
2. Solve the following system of inequalities graphically: 3x+2y⩽12,x⩾1,y⩾2
Ans: 3x+2y⩽12……(1) x⩾1…(2) y⩾2.……(3) The graphs of the lines, 3x+2y=12,x=1, and y=2, are drawn in the figure below. Inequality (1) represents the region below the line, 3x+2y=12 (including the line 3x+2y=12 ). Inequality (2) represents the region on the right side of the line, x=1 (including the line x=1 ). Inequality (3) represents the region above the line, y=2 (including the line y=2) As a result, the solution of the given system of linear inequalities is represented as follows by a common shaded region that includes the points on the various lines.
3. Solve the following system of inequalities graphically: 2x+y⩾6,3x+4y⩽12
Ans: 2x+y⩾6……(1) 3x+4y⩽12……(2) The graph of the lines, 2x+y⩾6 and 3x+4y=12, are drawn in the figure below. Inequality (1) represents the region above the line, 2x+y=6 (including the line 2x+y=6 ), and inequality (2) represents the region below the line, 3x+4y=12 (including the line 3x+4y=12 ). As a result, the solution of the given system of linear inequalities is represented as follows by a common shaded region that includes the points on the various lines.
4. Solve the following system of inequalities graphically: x+y⩾4,2x−y>0
Ans: x+y⩾4……(1) 2x−y>0……(2) The graph of the lines, x+y=4 and 2x−y=0, are depicted in the diagram below. The region above the line is represented by inequality (1) , x+y=4 (including the line x+y=4 ). It is observed that (1,0) satisfies the inequality, 2x−y>0.[2(1)−0=2>0] Therefore, inequality (2) represents the half plane corresponding to the line, 2x−y=0, containing the point (1,0) excludingtheline$2x−y>0$. As a result, the solution of the above system of linear inequalities is represented by thecommonshaded region as follows, which includes the points on line x + y =4 but excludes the points on line 2x - y = 0.
5. Solve the following system of inequalities graphically: 2x−y>1,x−2y<−1
Ans: 2x−y>1…(1) x−2y<−1….(2) The graphs of the lines, 2x−y=1 and x−2y=−1, are drawn in the figure below. Inequality (1) represents the region below the line, 2x−y=1 ( excluding the line 2x−y=1 ). and inequality (2) represents the region above the line, x−2y=−1,( excluding the line x−2y=−1 ). Hence, the solution of the given system of linear inequalities is represented by the common shaded region excluding the points on line as follows.
6. Solve the following system of inequalities graphically: x+y⩽6,x+y⩾4
Ans: x+y⩽6……(1) x+y⩾4……(2) Putting y=0 in (1) , Putting x=0 in (1) x+0=6,0+y=6 x=6,y=6 The graph of the lines, x+y=6 and x+y=4, are depicted in the diagram below. The region below the line is represented by inequality (1). , x+y=6 (including the line x+y=6 ), and inequality (2) represents the region above the line, x+y=4 (including the line x+y=4 ). As a result, the solution of the given system of linear inequalities is represented as follows by a common shaded region that includes the points on the various lines.
7. Solve the following system of inequalities graphically: 2x+y⩾8,x+2y⩾10
Ans: 2x+y=8……(1) x+2y=10 ….(2) Putting x=0 in (1) 2(0)+y=6 0+y=6 y=8 Putting y=0 in (1) 2x+(0)=6 2x=8 x=82 x=4 The graph of the lines, 2x+y=8 and x+2y=10, are drawn in the figure below. Inequality (1) represents the region above the line, x+2y=8, and inequality (2) represents the region above the line, x+2y=10. As a result, the solution to the given system of linear inequalities is written as follows:
8. Solve the following system of the inequalities graphically: x+y⩽9,y>x,x⩾0
Ans: First we solve x+y≤9 Putting x=0 in (1) 0+y=9 y=9 Putting y=0 in (1) x+0=9 x=9 Checking for (0,0) Putting x=0,y=0 x+y≤9 0+0≤9 0≤9 which is true.Hence origin lies in plane x+y≤9 So, we shade left side of line. Now we solve y>x Lets first draw graph of y=x Putting x=0 in (2) y=0 Putting x=2 in (2) y=2 Checking for (9,0) Putting x=9,y=0 y>x 0>9 which is false Hence (9,0) does not lie in plane x>y So, we shade the left side of the line. Also, x≥0 So, we shade the right side of the y axis. Hence the shaded region represents the given inequality
9. Solve the following system of inequalities graphically: 5x+4y⩽20,x⩾1,y⩾2
Ans: First we solve 5x+4y≥20
Let first draw graph of

5x+4y=20
Putting x=0 in (1)
5(0)+4y=20
0+4y=20
4y=20
y=204
y=5
Putting y=0in(1)
5x+4(0)=20
5x+0=20
5x=20
x=205
x=4
Drawing graph

Points to be plotted are (0,5),(4,0)
Points to be plotted are (0,5),(4,0)
Checking for (0,0)
5x+4y≤20
Putting x=0,y=0
5(0)+4(0)≤20
0≤20
Which is true
Hence origin lies in plane 5x+4y≤20
So, we shade left side of line
Also, y≥2
So, for all values of
x, where y=2

Points to be plotted are (0,2),(−1,2),(4,2)
Also, x≥1
So, for all values of y, where x=1

Point to be plotted are (1,0),(1,−1),(1,3)
Hence the shaded region represents the given in equality
10. Solve the following system of inequalities graphically:
3x+4y⩽60,x+3y⩽30,x⩾0,y⩾0
Ans: Now we solve 3x+4y≤60 Lets first draw graph of3x+4y=60 Putting x=0 in (1) 3(0)+4y=60 0+4y=60 4 y=60 y=604 y=15 Putting y=0 in (1) 3x+4(0)=60 3x+0=60 3x=60 x=603 x=20 Points to be plotted are (0,15),(20,0) Checking for (0,0) Putting x=0,y=0 3x+4y≤60 3(0)+4(0)≤60 0≤60 which is true Hence origin lies in plane 3x+4y≤60 So, we shade left side of line Now we solve x+3y≤30 Lets first draw graph of x+3y=30 Putting x=0 in (2) 0+3 y=30 3 y=30 y=303 y=10 Putting y=0 in (2) x+3(0)=30 x+0=30 x=30 Points to be plotted are (0,10),(30,0) Checking for (0,0) Putting x=0,y=0 x+3y≤30 0+3(0)≤30 0≤30 which is true Hence origin lies in plane x+3y≤30 So, we shade left side of line. Also given that x≥0,y≥0 Hence the shaded region will lie in the first quadrant. Hence the shaded region represents the given inequality.
11. Solve the following system of inequalities graphically:
2x+y⩾4,x+y⩽3,2x−3y⩽6
Ans: The set of inequalities are given as, 2x+y≥4 x+y≤3 2x−3y≤6 Simplifying 2x+y≥4 by substituting different values of x and y. When x=0, then, y=4 When y=0, then, x=2 So, the coordinates are (0,4) and (2,0). Now, if x=0 and y=0, then, 0≥4 Which can never be true, so the graph will be shaded away the origin. Simplifying x+y≤3 by substituting different values of x and y. When x=0, then, y=3 When y=0, then, x=3 So, the coordinates are (0,3) and (3,0). Now, if x=0 and y=0, then, 0≤3 Which is true, so the graph will be shaded towards the origin. Simplifying 2x−3y≤6 by substituting different values of x and y. When x=0, then, y=−2 When y=0, then, x=3 So, the coordinates are (0,−2) and (3,0). Now, if x=0 and y=0, then, 0≤6 Which is true, so the graph will be shaded towards the origin.
12. Solve the following system of inequalities graphically:
x−2y⩽3,3x+4y⩾12,x⩾0,y⩾1
Ans: First we solve x−2y≤3
Lets first draw graph of
x−2y=3
Putting x=0 in (1)
0−2y=3
−2y=3
y=3−2
y=−1.5
Putting y=0in(1)
x−2(0)=3
x−0=3
x=3
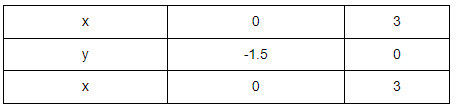
Points to be plotted are
(0,6),(3,0)
Checking for (0,0)
Putting x=0,y=0
x−2y≤3
0−2(0)≤3
0≤3
Which is true Hence origin lies in plane x−2y≤3
So, we shade left of line
Now we solve 3x+4y≥12
Lets first draw graph of
3x+4y=12
Putting x=0 in (1)
3(0)+4y=12
0+4y=12
4y=12
y=124
y=3
Putting y=0in(1)
3x+4(0)=12
3x+0=12
3x=12
x=123
x=4

Points to be plotted are
(0,3),(4,0)
checking for (0,0)
Putting x=0,y=0
3+4y≥12
3(0)+2(0)≥12
0≥12
which is false
Hence origin does not lie in plane 3x+2y>6
So, we shade rights side of line.
Also y≥1
So, for all values x

Points to be plotted are
(0,1),(−1,1),(4,1)
Also x≥0
So, the shaded region will lie on the right side of y-axis Hence the shaded region represents the given inequality.
13. Solve the following system of inequalities graphically: 4x+3y⩽60,y⩾2x,x⩾3,x,y⩾0
Ans: 4x+3y⩽60……(1) y⩾2x…−(2) x⩾3……….(3) Putting x=0 in (1) 4(0)+3y=60 0+3y=60 3y=60 y=603 y=20 Putting y=0 in (1) 4x+3(0)=60 4x+0=60 4x=60 x=604 x=15 Points to be plotted are (0,20),(15,0) Checking for (0,0) Putting x=0,y=0 4x+3y≤60 4(0)+3(0)≤60 0≤60 which is true Hence origin lies in plane 3x+4y≤60 So, we shade the left side of the line. Now we solve y≥2x Putting x=0 in (1) y=2(0) y=0 Putting x=2 in (1) y=2(2) y=4 Points to be plotted are (0,20),(15,0) Checking for (0,15) Putting x=0, y=15 y≥2x 15≥2(0) 15≥0 which is true Hence (0,15) lies in plane y≥2x So, we shade left side of line Also, x≥3 So, for all values of y,x=3 Given x≥3 so we shade right side of line. Also, given x,y≥0 So, the shaded region will line in 1st quadrant Hence the shaded region represents the given inequality.
14. Solve the following system of inequalities graphically:
3x+2y⩽150,x+4y=80,x⩽15,y⩾0,x⩾0
Ans: 3x+2y⩽150……..(1) x+4y=80……(2) x⩽15…(3) 3x+2y≤150 x+4y≤80 x≤15 y≥0 x≥0 Draw 3x+2y=150 check (0,0) Draw x+4y=80 check (0,0) Draw x=15 take left sides of x x≥0,y≥0, hence only 1 st Quadrant Intersection area is shaded.
15. Solve the following system of inequalities graphically:
x+2y⩽10,x+y⩾1,x−y⩽0,x⩾0,y⩾0
Ans: x+2y⩽10……….(1) x+y⩾1……..(2) x−y⩽0……..(3) The graph of the lines, x+2y=10,x+y=1 and x−y=0, are drawn in the figure below. Inequality (1) represents the region below the line, x+2y=10 (including the line x+2y=10). Inequality (2) represents the region above the line, x+y=1 (including the line x+y=1 ). Inequality (3) represents the region above the line, x−y=0 (including the line x−y=0 ). Since x⩾0 and y⩾0, The solution of the following system of linear inequalities is represented by every point in the common shaded region in the first quadrant, including points on the relevant lines and axes.
Last Updated on: December 05, 2025
